슈퍼 헥사곤 UV 셰이더(Super Hexagon UV Shader)

개요

uv로 기본도형인 정육각형을 작도하는 기본기에 대한 포스팅입니다. 그리고 이를 응용하여 타일링하는 방법에 대해 배워보도록 하겠습니다.

float2 uv = (i.uv - 0.5);
col.rgb = float3(uv, 0);

먼저 중앙으로 ${0.5}$만큼 움직인 uv를 준비합니다.

float2 uv = abs(i.uv - 0.5);

색을 눈으로 디버깅 할 수 있게 abs() 절댓값 함수로 음수를 제거하여 대칭 하였습니다.

정육각형 도형을 작도 하려면 먼저 도형의 성질을 이해해야 합니다.

정육각형은 여섯개의 변을 가지고 있고, 한 각의 크기는 ${120˚}$ 입니다. 즉 정육각형 세개를 모으면 합이 ${360˚}$ 가 되어 UV 타일링(Tilling)을 할 경우 테셀레이션(tessellation, 모델링 용어의 그 테셀레이션 맞습니다)이 가능합니다.

도형을 더 작은 구성요소로 분해 해봅시다. 그러면 정삼각형 여섯개로 이루어진 도형과 마찬가지입니다.

더 작게 나눠서 생각해보면, 정삼각형 안에는 직삼각형이 들어있습니다.

피타고라스 정리

직삼각형에 대한 피타고라스 정리에 따라서, ${x}$값은 정육각형 한 변의 길이의 절반입니다.

값이 절반이니까 좀 더 알아보기 쉽게, 직삼각형을 두배로 키우면 이렇게 됩니다.

정육각형에 외접하는 원을 그려봅시다. 지름은 자연스레 ${z}$값 입니다.

정육각형은 정삼각형으로 이루어져 있습니다. 그리고 정삼각형의 모든 변의 길이는 같습니다. 따라서 반지름은 ${x}$입니다.

그리고 지름은 반지름의 두배니까, ${z}$값은 ${2x}$와 같습니다.

그래서 반지름을 ${1}$으로 하고 지름을 두 배인 ${2}$로 가정합니다.

피타고라스 정리에 의해서, ${y}$의 값은 ${\sqrt{3}}$입니다.

회전 행렬

float c = cos(Radians);
float s = sin(Radians);
float2 rotateMatrix = float2(s, c);
float result = dot(uv, rotateMatrix);

\[u(x) * s + v(y) * c\]

회전에 대해 다룬 포스트에서 회전행렬과 내적 연산을 통해 uv를 회전 시킬 수 있다는 것을 배웠습니다.

float2 uv = abs(i.uv - 0.5);
 float Degrees2Rad = UNITY_PI * 2 / 360;
 float Radians = _Radians * Degrees2Rad;
 float c = cos(Radians);
 float s = sin(Radians);
 uv = dot(uv, normalize(float2(s, c)));

uv = dot(uv, normalize(float2(1, 1)));

${sin(90)}$, ${cos(0)}$을 계산하여 회전 행렬을 만들면 값은 float2(1,1)과 같습니다. 내적을 하면 uv는 정확히 ${45˚}$ 만큼 회전합니다.

uv = step(uv, 0.2);

회전 각이 얼마인지 눈으로 쉽게 보며 디버깅 할 수 있게 step() 으로 값을 uv값을 적당히 끊어주면 마름모 꼴을 얻을 수 있습니다.

uv = dot(uv, normalize(float2(sqrt(3), 1)));

아까 피타고라스의 정리로 구했던 ${\sqrt 3}$을 ${sin(90)}$대신 넣으면 정육각형 한 각의 크기인 ${120˚}$를 얻을 수 있습니다.

float hexa = dot(uv, normalize(float2(sqrt(3), 1)));

float hexa = dot(uv, normalize(float2(sqrt(3), 1)));
hexa = max(hexa, uv.y);

max() 함수를 이용하여 uv 세로축의 값으로 덮어 씌우면 정육각형 형태의 디스턴스 필드(Distance Field)가 나옵니다. 이제 uv를 타일링 해봅시다.

타일링 하기

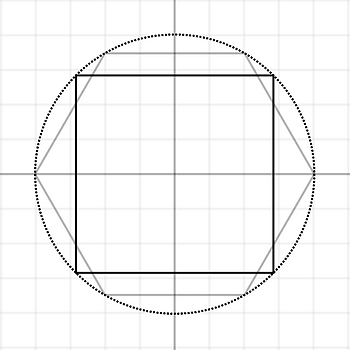
원에 내접하는 정사각형을 그려봅시다. 한 변의 길이는 ${1}$으로 가정합니다. 이것이 기존의 정사각형 형태의 uv입니다.

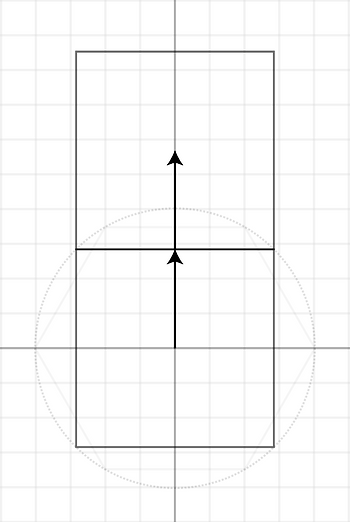
정사각형을 타일링 하는 것은 매우 쉽습니다. 단순히 한 변의 길이 ${1}$만큼 수직, 수평으로 움직이면 됩니다.

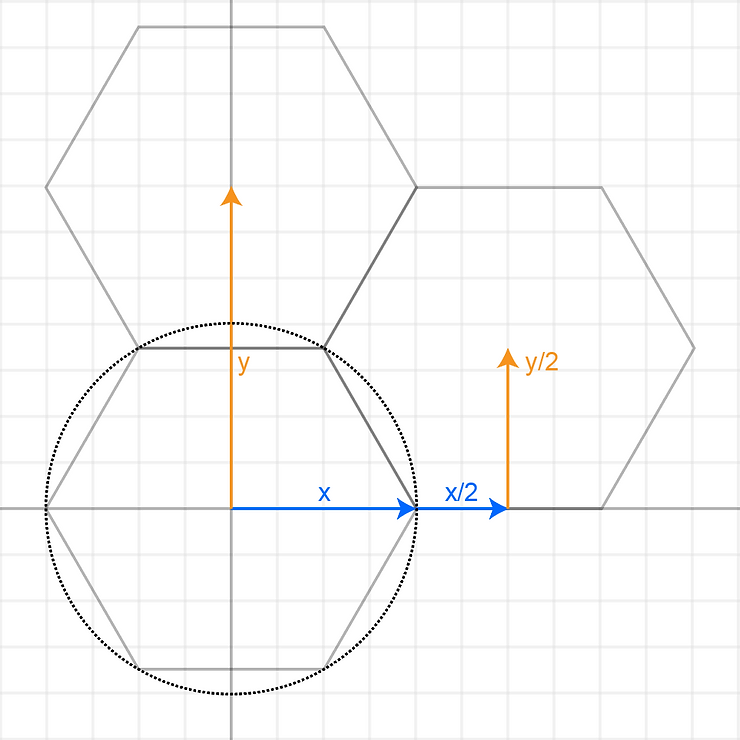
정육각형은 서로 각이 맞물려야 하기 때문에, ${y}$만큼 수직으로 움직이고, ${x + x/2}$ 만큼 수평으로 움직여야 합니다.

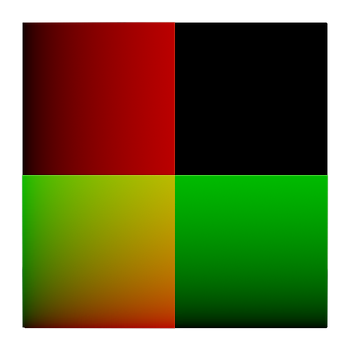
지금 상태에서는 문제에 어떻게 접근해야 할 지 감이 안옵니다.

하지만 문제를 단순화 하면 쉽게 풀 수 있습니다. 그러니 먼저 정사각형 타일링을 시도 해봅시다.

frac(n) 함수

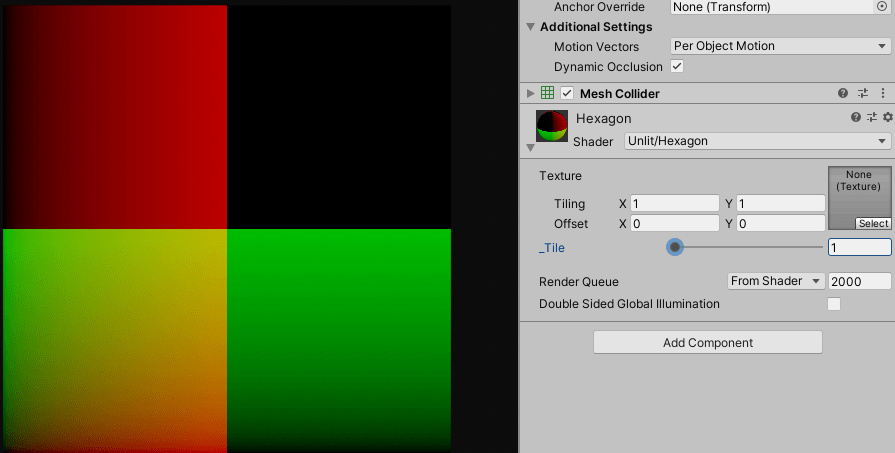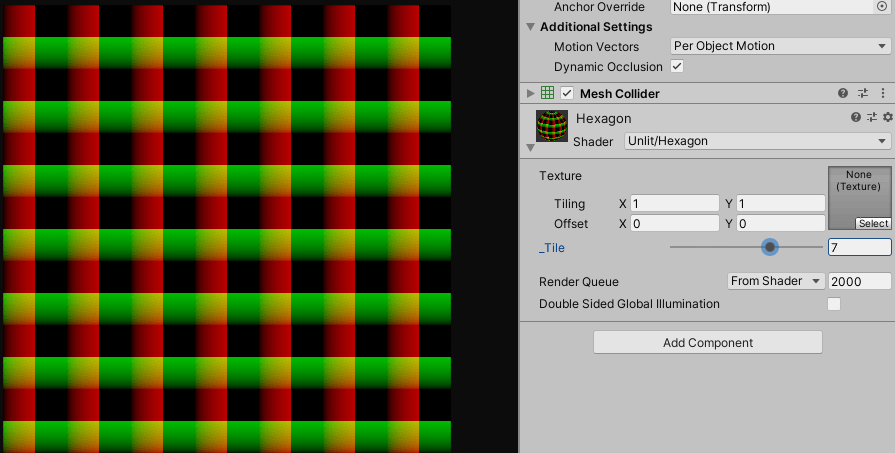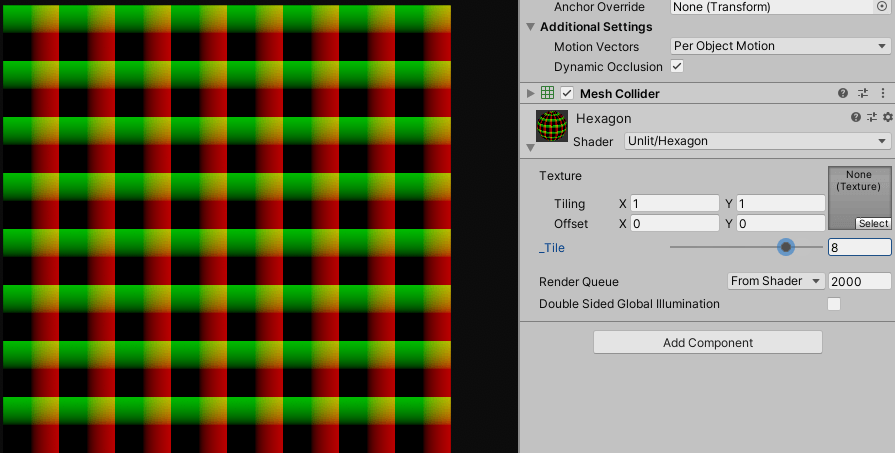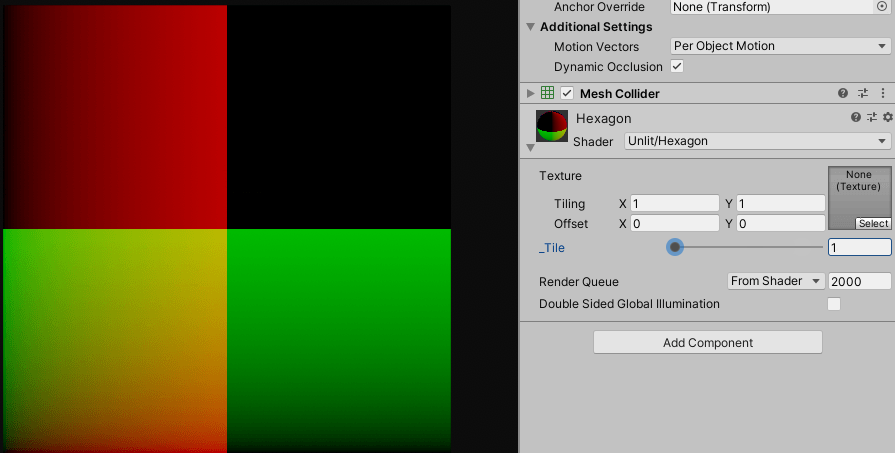
float2 uv = (i.uv - 0.5) * _Tile;
float2 B = frac(uv) -0.5;
col.rgb = float3(a, 0);

단순히 frac()함수를 통해서 ${0}$에서 ${1}$사이의 uv값이 반복되게 처리했습니다.

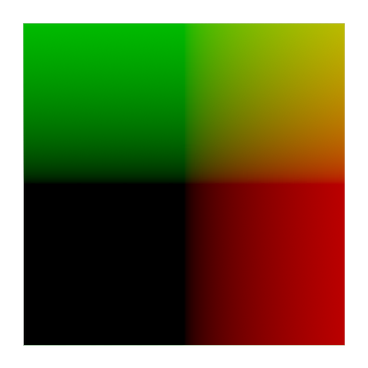
(float2 A = frac(uv - 0.5) - 0.5; / float2 B = frac(uv) - 0.5;)

float2 uv = (i.uv - 0.5) * _Tile;
float2 A = frac(uv - 0.5) - 0.5;
col.rgb = float3(b, 0);

같은 uv에서 ${-0.5}$ 만큼 수직, 수평 이동한 uv를 하나 더 만들어줍니다.

length(n) 함수

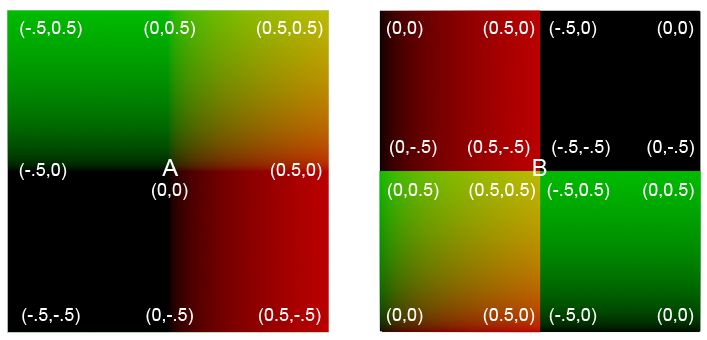
(length(A) / length(B))

length()함수로 원점 ${(0,0)}$에서 거리를 재면 위와 같은 데이터를 얻을 수 있습니다.

이렇게 얻어낸 거리 값을 아래와 같은 조건문으로 비교를 하면?

 if (length(a) < length(b))
     result = a;
 else
     result = b;

픽셀 단위로 비교해서, a의 값이 더 작으면 a를 반환하고, 그렇지 않으면 b를 반환합니다.

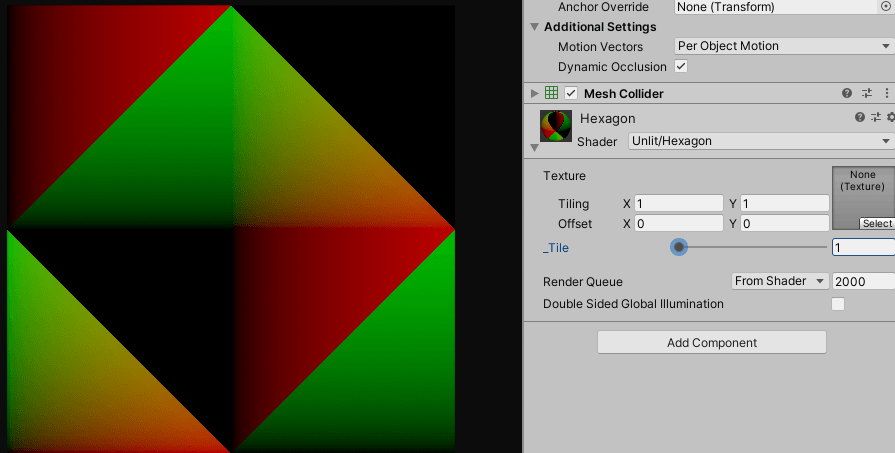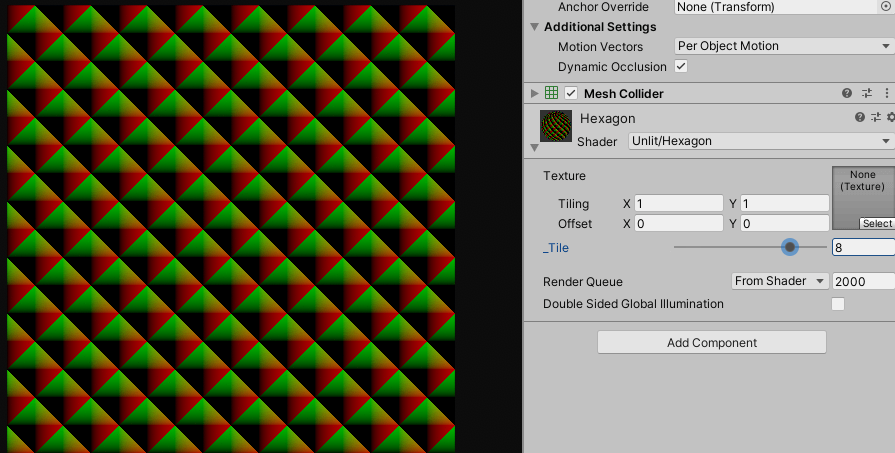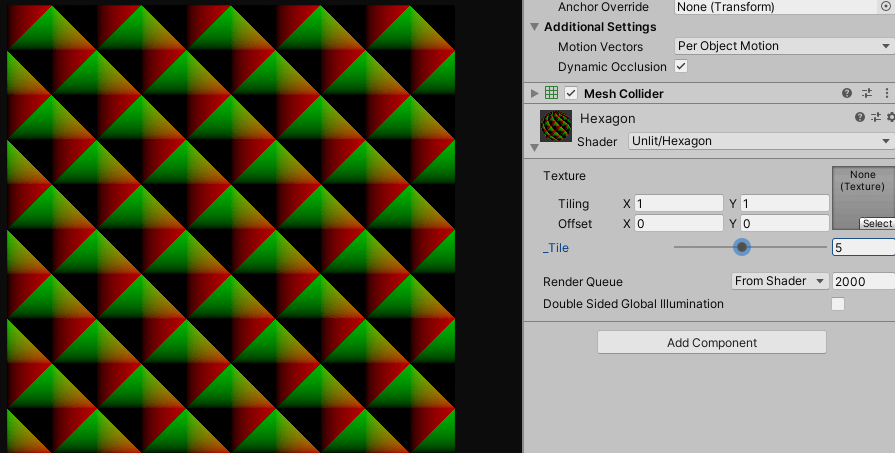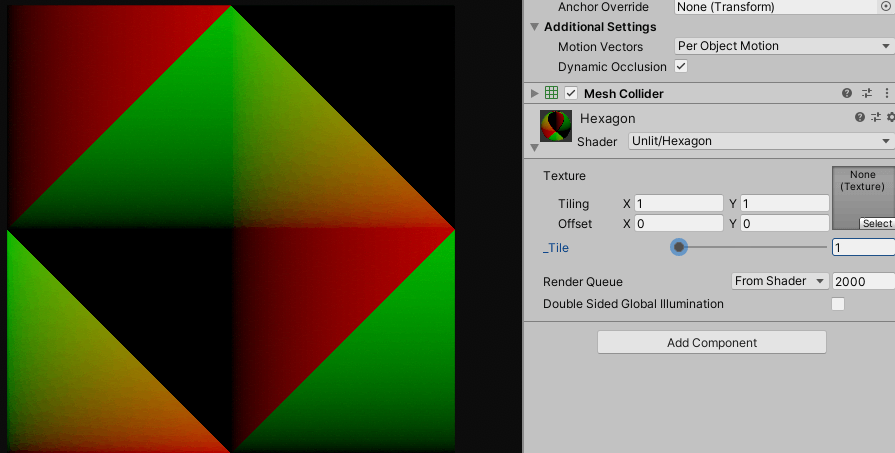
타일링이 잘 되는 것을 확인 할 수 있습니다. 같은 방법으로 정육각형도 처리하면 됩니다.

셰이더 연산 부하를 줄이기 위해 삼항연산자로 if를 쓰지 않고 더 줄일 수도 있습니다만, 가독성을 위해서 이렇게 처리하고 넘어가겠습니다.

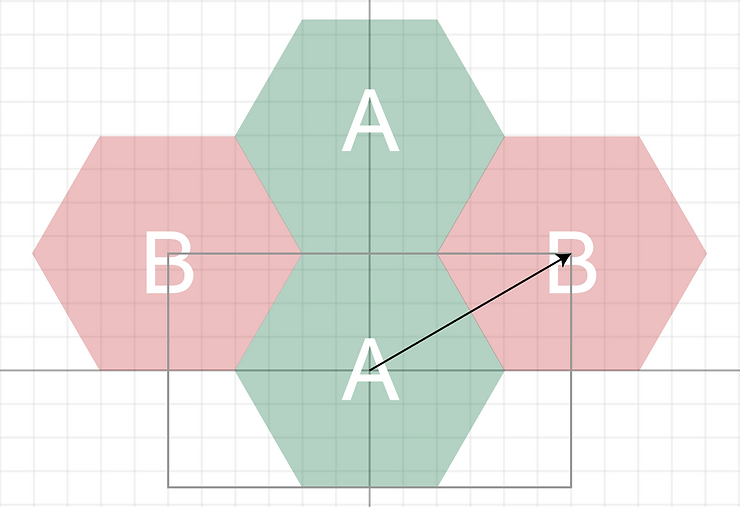
정사각형과 같은 아이디어로, uv를 정사각형에서 변경하여 직사각형으로 만들고, uv A와 uv B를 위와 같은 식으로 배치하면 타일링이 될 것입니다.

문제는 frac() 함수로 값을 ${1}$ 미만으로 자르는 것은 한 변의 길이가 ${1}$인 정사각형 타일링에만 사용할 수 있습니다.

지금처럼 가로 길이가 ${1}$을 넘는 직사각형으로 만들려면 ${1}$을 넘는 값만큼 uv를 자를 수 있는 함수가 필요합니다.

fmod(A,B) 함수

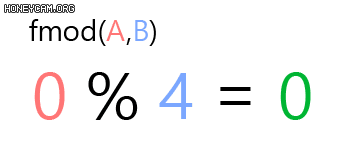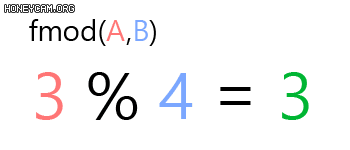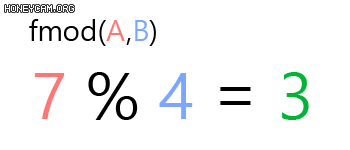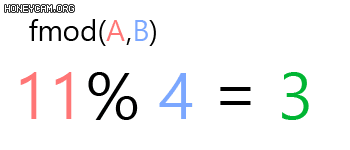
Modulo(혹은 Modulus, Mod) 함수 fmod(,)는 ${A}$를 ${B}$로 나누고 남은 나머지 값을 반환합니다.

예를 들어 fmod(1, 4) ${= 1}$입니다. ${4}$가 ${1}$보다 크기 때문에 나누지 못하니까요.

연산기호로 하면 %로 표현됩니다.

저희는 나머지를 계산하는 fmod() 함수에 대해 포스트(링크)에서 배웠습니다.

float2 uv = (i.uv - 0.5) * _Tile;

a = frac(uv - 0.5) - 0.5;
b = frac(uv) - 0.5;

a = fmod(uv - 0.5, 1) - 0.5;
b = fmod(uv, 1) - 0.5;

생각해봅시다. frac()은 ${1}$ 미만의 값을 끊어주니까, 사실상 uv를 ${1}$으로 나눈 나머지 값을 반환하는 것과 같습니다. 정확히 fmod(n, 1)과 같은 결과를 반환 해야합니다.

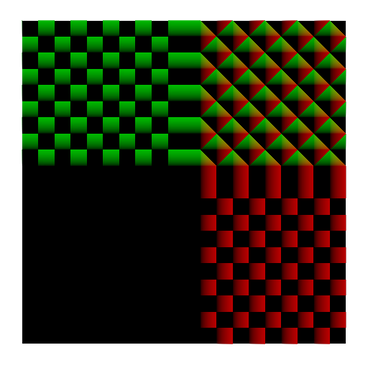
(fmod(,) / frac())

하지만 두 함수의 결과물은 이렇게 큰 차이가 있는데, 유니티에서 fmod(,)는 나머지 값이 음수일 경우 그대로 음수로 반환하기 때문에 생기는 오류입니다.

float2 uv = (i.uv + 0.5) * _Tile; // 음수 제거

따라서 음수부분을 없애주기 위해서, ‘${uv - 0.5}$’ 가 아닌 ‘${uv + 0.5}$’로 고쳐줘야 합니다.

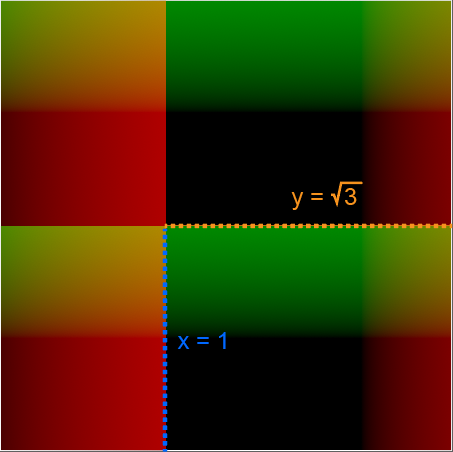
float2 uv = (i.uv + 0.5) * _Tile;

float2 ratio = normalize(float2(sqrt(3), 1));
float2 halfRatio = ratio * 0.5;

float2 b = fmod(uv, ratio) - halfRatio;

수직,수평 이동해야할 직사각형의 비율을 설정해보겠습니다.

${1}$만큼 수직, ${\sqrt{3}}$ 만큼 수평 이동한 벡터를 fmod(,)로 연산합니다.

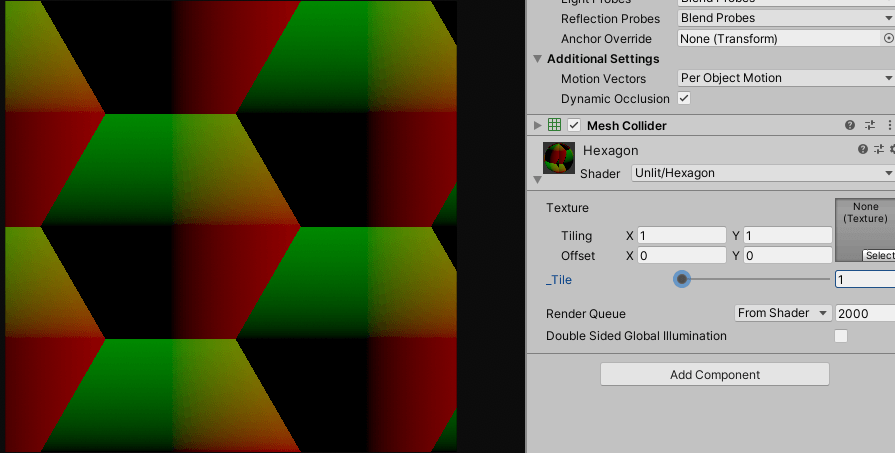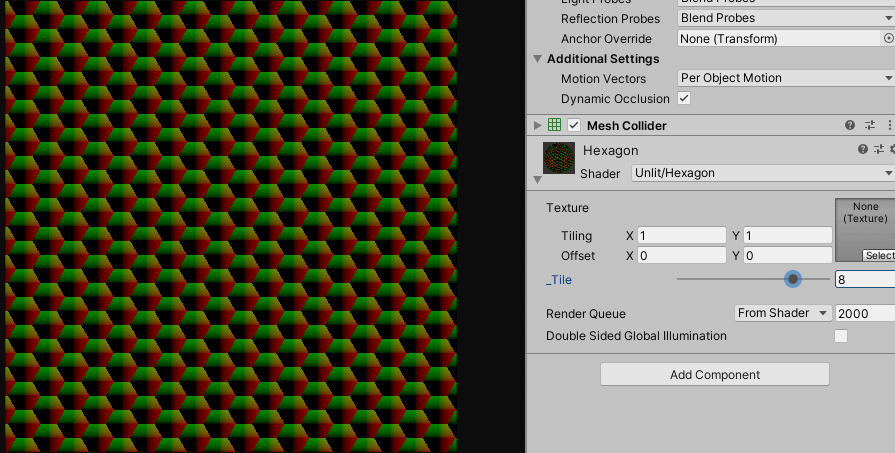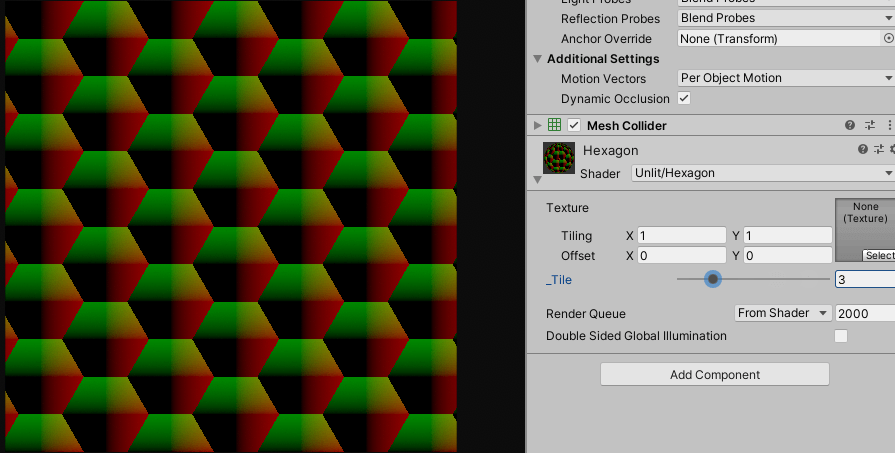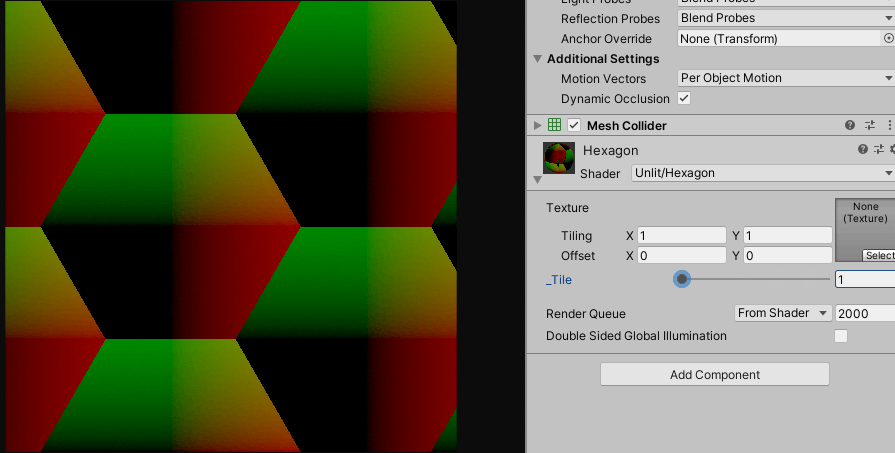
float2 uv = (i.uv + 0.5) * _Tile;

float2 ratio = normalize(float2(sqrt(3), 1));
float2 halfRatio = ratio * 0.5;

float2 a = fmod(uv - halfRatio, ratio) - halfRatio;
float2 b = fmod(uv, ratio) - halfRatio;

if(length(a) < length(b))
    result = a;
else
    result = b;

같은 방식으로 절반의 비율 만큼 이동한 uv를 만들어주고 조건문으로 합쳐주면 잘 동작합니다.

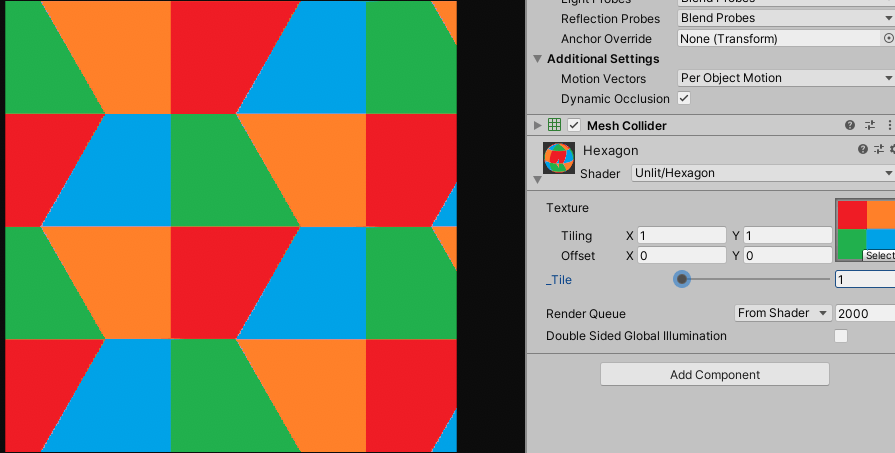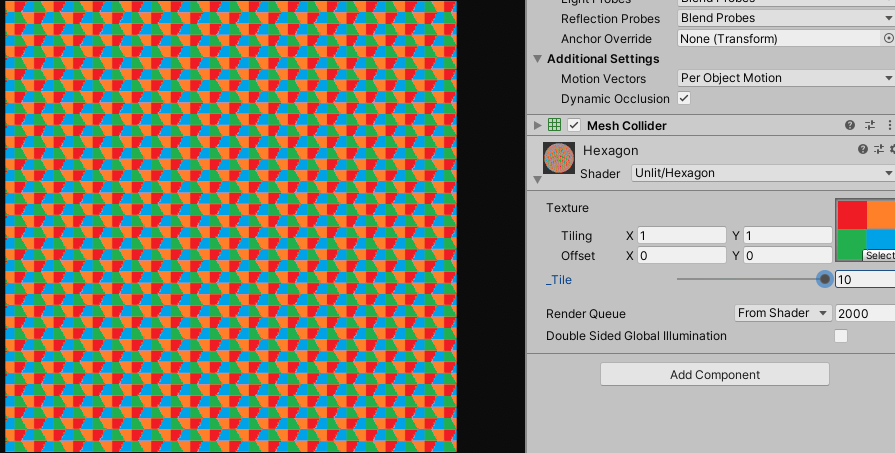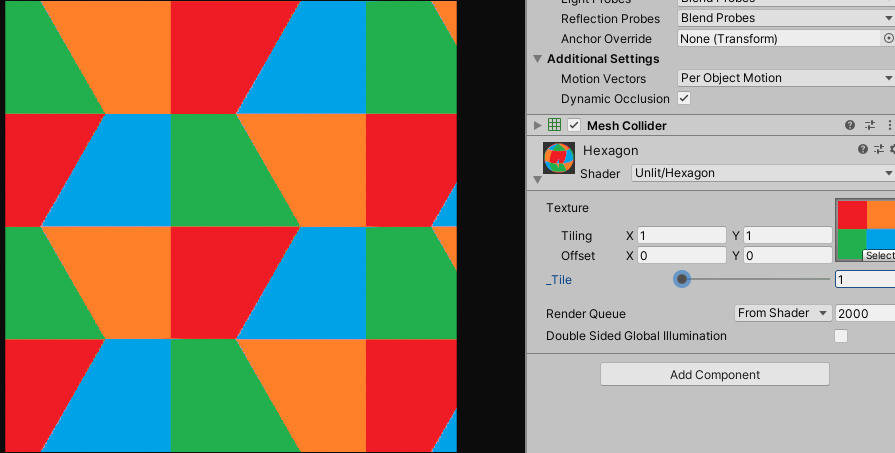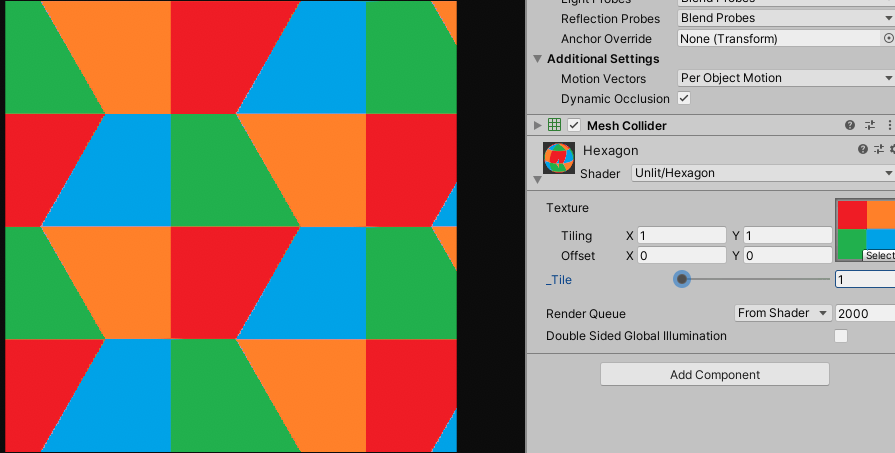
(텍스쳐를 넣은 경우)

제가 만든 방식은 uv가 ${180˚}$ 회전 되어 있긴 한데 큰 문제는 아니니 필요하시면 수정해서 사용해주세요.

헥사곤 이펙트(Hexagon Effect)

float HexaDistance(float2 uv)
{
  uv = abs(uv);
  float hexa = dot(uv, normalize(float2(sqrt(3), 1)));
  hexa = max(hexa, uv.y);
  return hexa;
}

정육각형의 디스턴스 필드를 출력했던 부분을 함수로 분리합니다. uv가 회전 되어 있긴 하지만 정육각형의 중심에 원점이 있으니 그대로 사용해도 동작합니다.

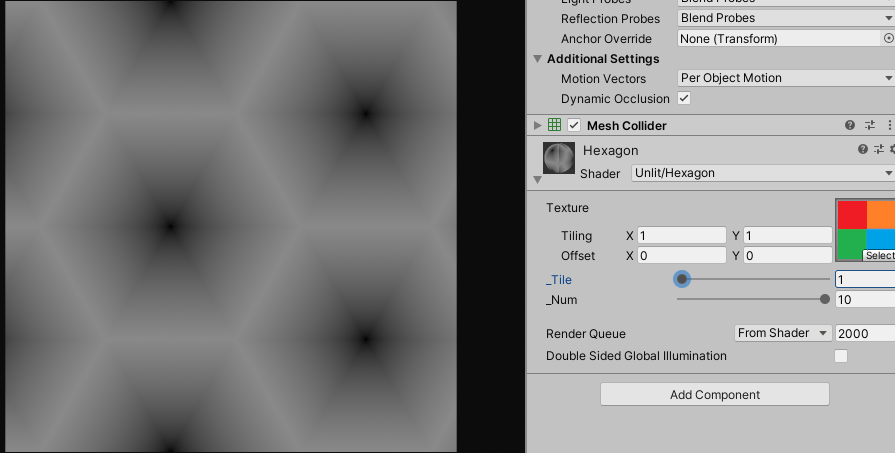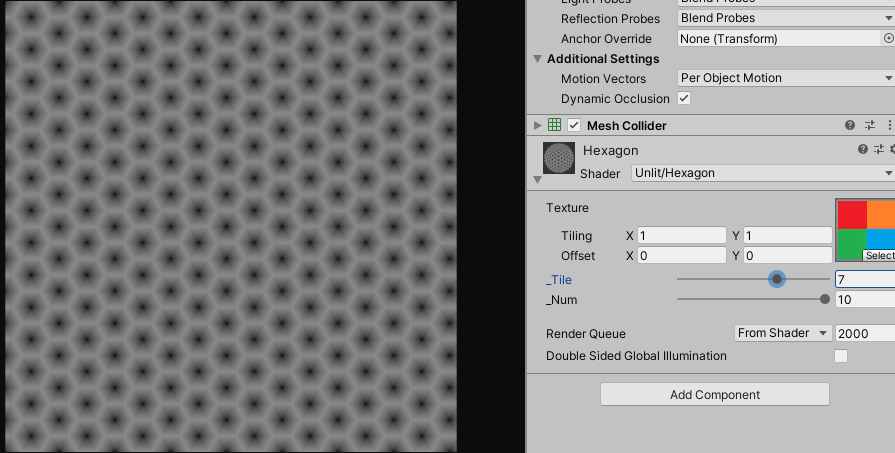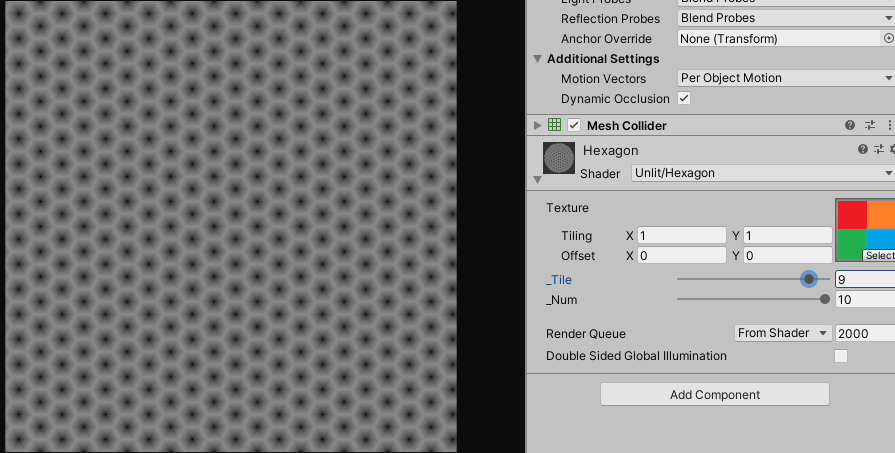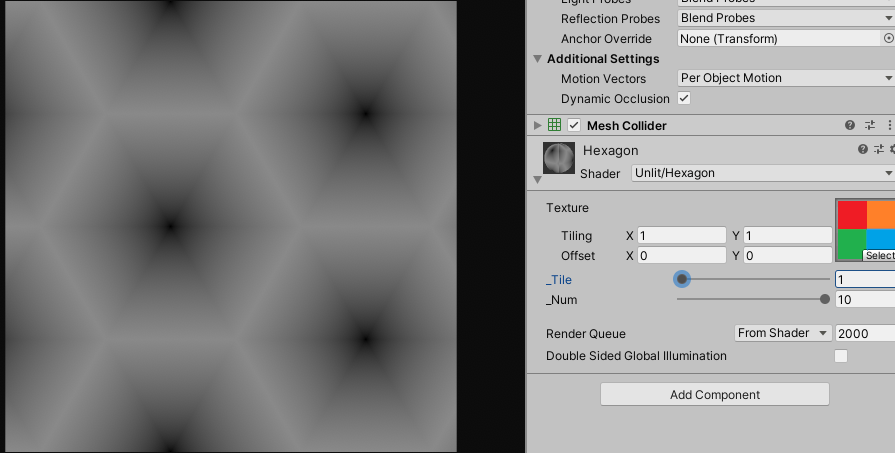
 float distanceField = HexaDistance(result);
 float2 output = float2(result.x, distanceField);
 return output;

사실 게임에서 이런 종류의 이펙트를 사용할 때는, 포스트 내용처럼 디스턴스 필드나 uv를 수학으로 계산하여 처리하지 않고 연산 부하를 줄이기 위하여 대부분 텍스쳐로 베이크(Bake)해서 사용합니다.

이렇게 만들어진 디스턴스 필드에 프랙탈 노이즈(Fractal Noise) 텍스쳐를 사용하거나 다른 방법으로 랜덤성을 부여해서, 여러가지 효과의 셰이더를 작성 할 수 있습니다.

끝까지 읽어주셔서 감사합니다. 여러분의 관심이 제게 큰 도움이 됩니다.