이전 포스트에서 벡터 공간의 사칙연산을 활용해 벡터의 움직임을 구현했습니다. 하지만 직선적인 움직임만 표현할 수 있었습니다. 이번에는 회전에 대해서 살펴보겠습니다.
회전은 원의 궤적을 따라 이동하는 움직임이기 때문에 이를 이해하려면 원과 밀접하게 연결되어있는 삼각함수를 알아야 합니다. 삼각함수의 정의부터 시작해서 단위 원을 활용해 삼각함수의 성질과 주요 공식을 학습할 것입니다.
삼각함수가 만들어내는 회전의 성질을 활용해 다양한 효과를 만들어내는 원리에 대해서 알아봅시다.
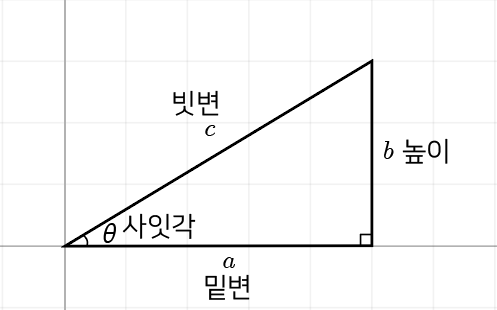
한 각이 직각(${90˚}$)인 직각삼각형을 이루는 세 변은 각 위치에 따라 밑변(${a}$), 높이(${b}$), 빗변(${c}$)이라고 부릅니다.
한 각이 직각이므로 나머지 두 각의 합이 ${90˚}$가 되어야 합니다. 따라서 두 각은 모두 ${90˚}$ 보다 작은 예각입니다.
빗변과 밑변의 사잇각은 기호 (${\theta}$)를 이용해 나타냅니다.
직각삼각형을 구성하는 세 변에서 두 변을 뽑아 각각의 비례 관계를 나타낸 것을 삼각비(trigonometric Ratio)라고 합니다.
삼각비에는 여러 종류가 있지만 사인(Sine), 코사인(Cosine), 탄젠트(Tangent) 세 가지가 가장 대표적입니다.
\[sin \theta = \frac{b}{c} \\ cos \theta = \frac{a}{c} \\ tan \theta = \frac{b}{a}\]밑변의 길이를 ${a}$, 높이를 ${b}$, 빗변의 길이를 ${c}$, 빗변과 밑변과의 사잇 각을 ${\theta}$라고 할 때, 각 삼각비의 관계는 위와 같이 분수식으로 표현할 수 있습니다.
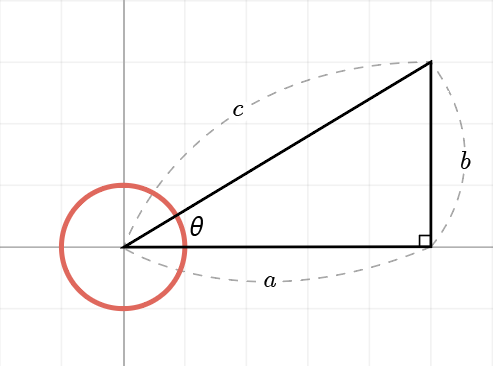
직각 삼각형에서 측정할 수 있는 사잇각은 ${0˚}$ 보다 크거나 ${90˚}$ 보다 작아야 합니다.
이때 위 이미지와 같이 직각 삼각형을 데카르트 좌표계 상에 배치하고 사잇각의 범위를 실수 전체로 확장한 대응 관계를 삼각함수(Trigonometric function)라고 합니다.
가장 많이 사용하는 삼각함수인 사인(Sine) sin() 함수와 코사인(Cosine) cos() 함수의 개념은 직각삼각형에서 출발했지만 원점을 중심으로 반지름이 1인 평면 위의 단위 원(Unit circle)을 사용해 나타내면 좀 더 쉽게 파악할 수 있습니다.
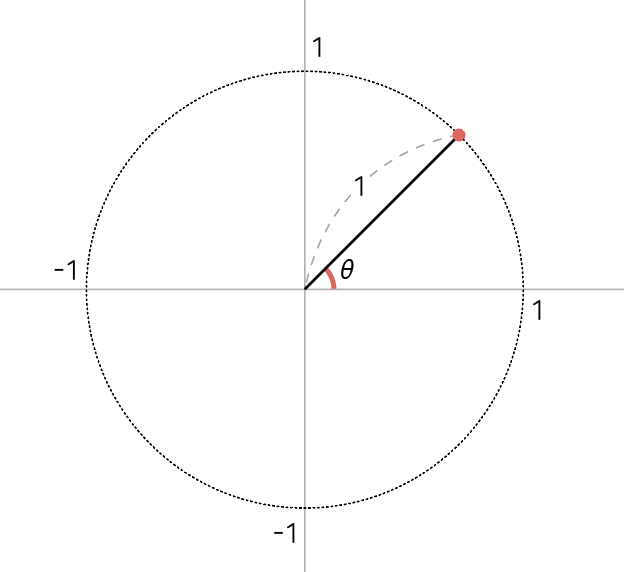
데카르트 좌표계에서 원점에서부터 제 ${1}$사분면의 단위 원의 원주 위에 있는 임의의 점을 이어 빗변을 그었습니다.
원의 반지름의 길이는 ${1}$이므로 이 빗변의 길이는 항상 ${1}$입니다. 그리고 ${x}$축과 해당 빗변이 이루는 각을 사잇각으로 지정합니다.
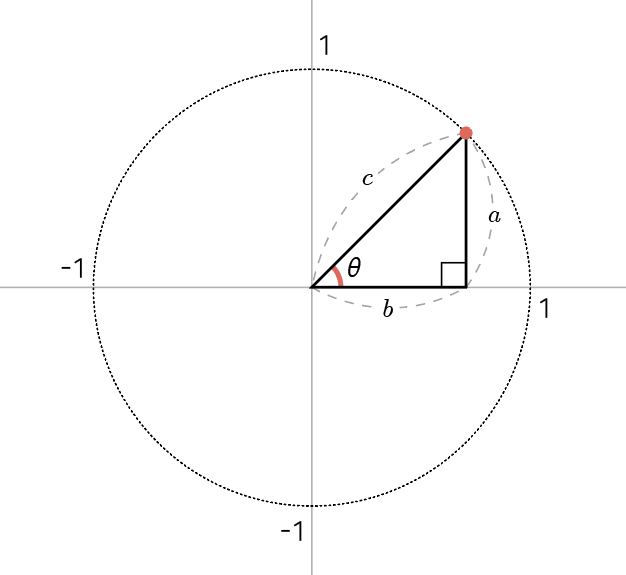
그런 다음에는 빗변에서 ${x}$축으로 수직선을 내려 직각 삼각형을 그려봅시다. 직각삼각형으로부터 삼각비를 계산 할 수 있을 것입니다.
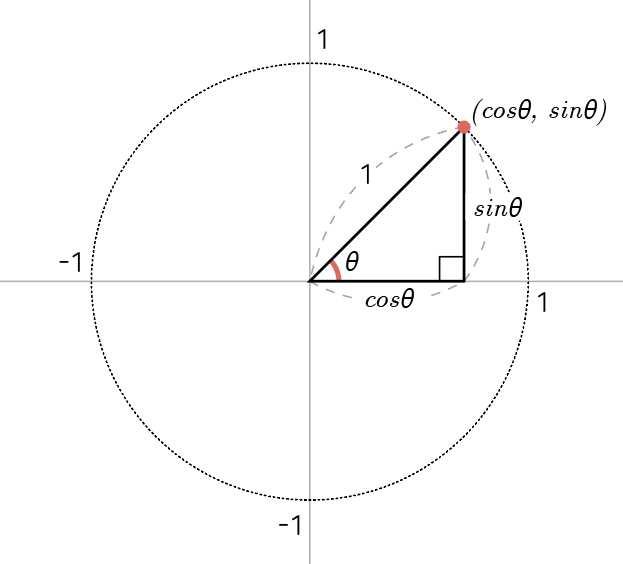
빗변 ${c}$의 길이가 ${1}$이므로 삼각비 ${sin\theta}$의 값은 높이 ${b}$와 같고, ${cos\theta}$의 값은 밑변 ${a}$와 같습니다.
따라서 데카르트 좌표계에서 빗변이 가리키는 단위 원의 좌표는 ${(sin\theta, cos\theta)}$로 표현할 수 있는데, 이를 삼각함수로 확장하면 원주 위의 모든 좌표는 ${(sin\theta, cos\theta)}$에 대응한다고 할 수 있습니다.
\[cos^{2}\theta + sin^{2}\theta = 1\]그렇다면 밑변 ${a}$의 ${x}$좌표는 ${cos\theta}$가 되고, 높이 ${b}$의 좌표는 ${sin\theta}$가 되는데 이를 피타고라스 정리 ${a^{2} + b^{2} = c^{2}}$에 대입하면 위와 같은 공식을 얻을 수 있습니다.
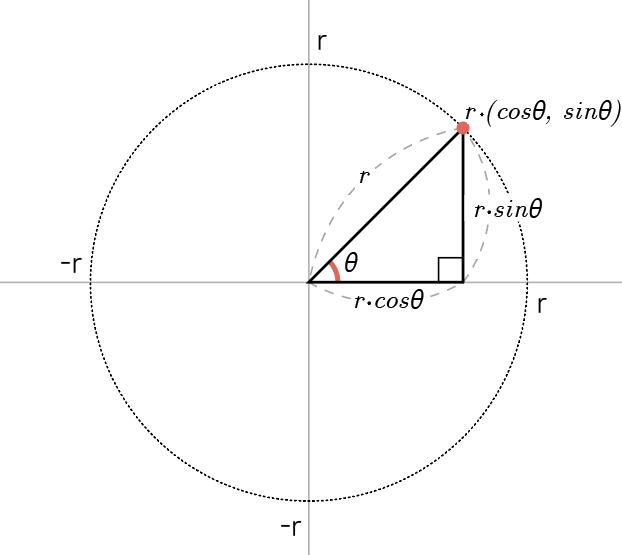
단위 원의 반지름 길이를 ${r}$으로 일반화 시켜서 생각해봅시다.
반지름이 ${r}$인 원에서의 빗변은 벡터의 개념으로 보았을 때 길이가 ${1}$인 벡터와 평행하고 길이는 ${r}$배 만큼 증가 했으므로 스칼라 곱셈에 의해 ${r * (cos\theta, sin\theta)}$라는 좌표를 갖게 됩니다.
이로써 빗변의 길이가 ${r}$인 직각삼각형의 밑변의 길이는 ${r * cos\theta}$가 되고, 높이의 길이는 ${r * sin\theta}$가 됨을 알 수 있습니다.
\[r^{2}(cos^{2}\theta + sin^{2}\theta) = r^{2} \\ \therefore cos^{2}\theta + sin^{2}\theta = 1\]앞서 구한 식은 반지름의 길이와 무관하게 동일하게 성립함을 알 수 있습니다.
이 식은 삼각함수의 기본을 이루는 중요한 공식으로, 이후 회전과 관련된 계산에 유용하게 사용되므로 암기해 두는 것을 권장합니다.
삼각함수의 성질
\[\vec{v} = (v_{x}, v_{y}) = (cos0, sin0) = (1,0) \\ \therefore sin0 = 0, cos0 = 1\]데카르트 좌표계에서 각도(angle)는 ${x}$축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를 의미합니다. 반지름이 ${1}$인 단위 원에서 반시계 방향의 회전을 생각해봅시다.
아직 회전하지 않아서 ${x}$축 상에 위치한 빗변 ${\vec{v}}$와의 좌표는 ${(1,0)}$인데, 이 각도는 ${0˚}$에 대응한다고 할 수 있습니다.
따라서 각도에 대한 sin()과 cos()의 값은 위와 같습니다.
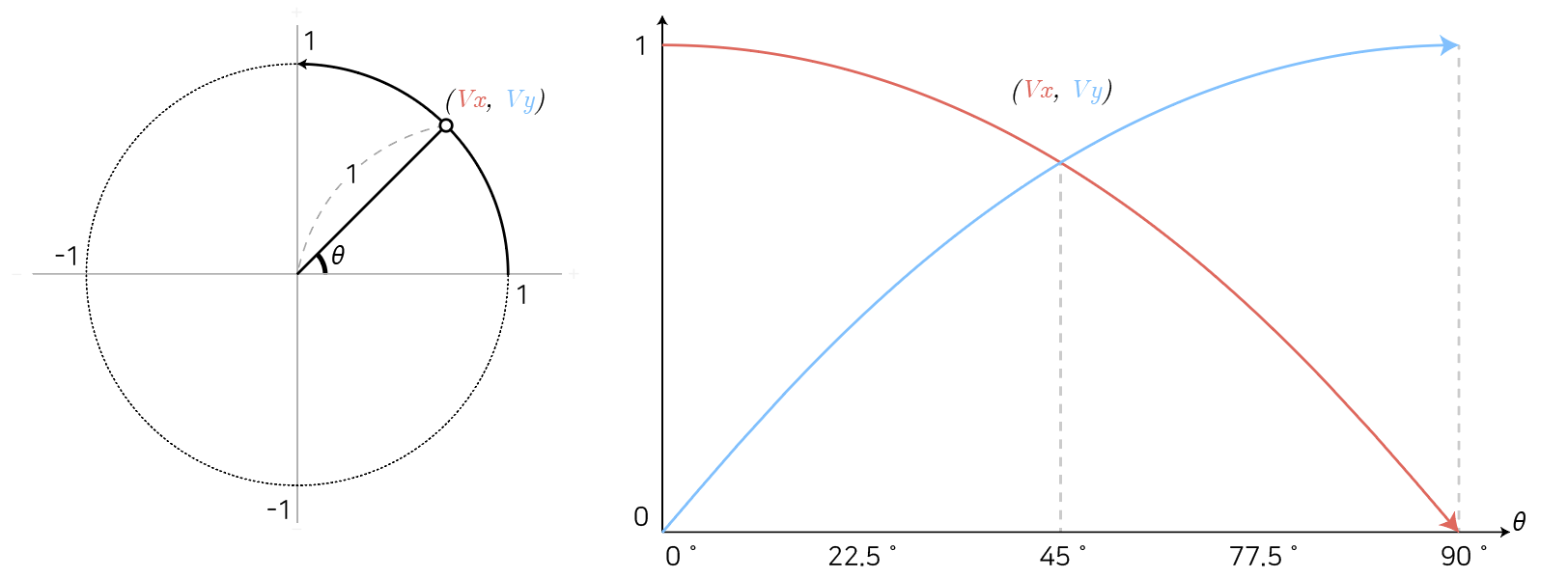
각도를 0도에서 90도까지 서서히 증가시키면서 회전하는 빗변의 좌표 ${v_{x}}$와 ${v_{y}}$의 변화를 살펴봅시다. 각도가 증가할수록 ${v_{x}}$값은 감소하고 ${v_{y}}$값은 증가합니다.
그리고 목적지인 90도에 도달하면 y축 상에 위치한 좌표 ${(0,1)}$과 일치하는 벡터가 만들어집니다.
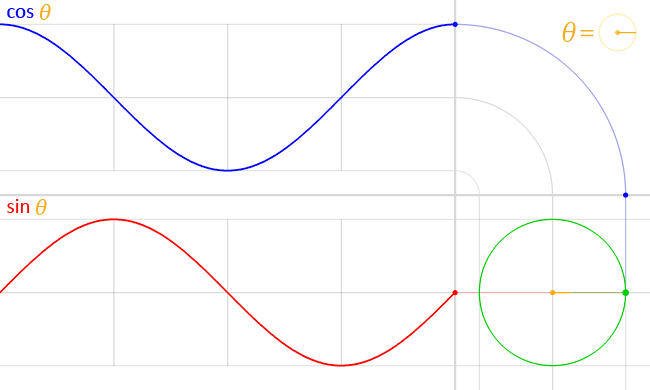
${v_{x}}$값을 빨간색으로, ${v_{y}}$값을 파란색으로 표시해서 좌표의 x값과 y값의 변화를 추적하면 부드러운 곡선이 만들어집니다.

각도가 ${90˚}$을 넘어서면 ${v_{x}}$값은 ${0}$을 지나 음수가 되고, ${v_{y}}$ 값은 다시 ${0}$을 향해 감소하기 시작합니다.
계속해서 한바퀴에 해당하는 ${360}$ 까지 빗변의 좌표 변화를 계속 관찰하면, ${-1}$에 도달할 때 까지 계속 감소하다가 ${-1}$에 도달하면 방향을 바꿔서 ${1}$을 향해 증가하며, ${1}$에 도달하면 다시 ${-1}$을 향해 감소하는 패턴을 반복합니다.
이런 값의 변화는 ${[-1, 1]}$ 범위 내에서 ${360}$ 마다 반복되는데, 변화값의 범위를 진폭(Amplitude), 반복되는 각도를 주기(Period)라고 합니다.
${360}$도 마다 이 패턴이 반복되므로

cos()에 대응하는 ${v_{x}}$값의 그래프는 위의 형태를 가집니다.

sin()에 대응하는 ${v_{y}}$값의 그래프는 위의 형태를 가집니다.
sin()과cos()은 항상 ${-1}$ 에서 ${1}$ 사이를 일정하게 반복하는 패턴을 띱니다.sin()과cos()의 값은 ${360˚}$ 주기로 반복됩니다.- y축을 기준으로 좌우를 접어 포갰을 때
cos()그래프는 데칼코마니 처럼 좌우 대칭인 반면,sin()그래프는 상하가 반전된 원점 대칭의 형태를 가집니다.
cos()와 같이 좌우 대칭의 성질을 가진 함수를 짝함수(Even function) 또는 우함수라고 부르며,
sin()와 같이 원점 대칭의 성질을 가진 함수를 홀함수(Odd function) 또는 기함수라고 부릅니다.
특히 ${3}$번에서 언급한 sin()과 cos() 그래프가 지니는 홀함수와 짝함수의 성질은 위의 식으로 정리할 수 있습니다.
이 역시 향후 회전에 관련된 계산에 유용하게 사용되므로 숙지해둡시다.
\[tan \theta = \frac{b}{a}\]이번에는 탄젠트(tangent) tan() 함수의 특징을 알아봅시다. tan()는 빗변과 무관하게 밑변과 높이의 관계만을 나타냅니다.
분자와 분모를 모두 빗변 값으로 각각 나누면 위와 같이 ${cos}$와 ${sin}$으로 ${tan}$을 표현할 수 있습니다.
분모의 값은 ${0}$이 될 수 없기 때문에 분모에 해당하는 cos() 값이 ${0˚}$이 되는 ${90˚}$에서는 tan() 값이 존재하지 않습니다.
이는 ${270˚}$인 경우에도 동일하고, ${-90˚}$, ${-270˚}$인 경우에도 마찬가지입니다. 그렇기 때문에 tan()의 정의역에는 해당 구간이 포함되지 않습니다.

위 이미지는 tan()의 그래프이며 sin()와 동일하게 홀함수의 성질을 지님을 알 수 있습니다.
각의 측정법
일상 생활에서 각의 크기를 잴 때 ${0}$에서 ${360}$까지의 수를 사용하는 각도법(Degree)을 사용합니다.
각도법에서 기준으로 삼는 ${360}$이라는 수는 약수가 많아 원을 다양한 방법으로 쪼개어 활용할 수 있기 때문인데,
이는 일상생활에서의 편의를 위한 것일 뿐 ${360}$이라는 값은 표준으로 사용하기에는 너무 큰 수입니다.
벡터의 경우 크기를 비교하기 용이하도록 크기 ${1}$의 단위 벡터를 정의한 것 처럼, 각을 측정할 때도 단위량 ${1}$을 기반으로 상대적인 크기를 측정할 수 있도록 체계를 만들면 합리적일 것입니다.
그래서 실무 계산에서 삼각함수를 응용할 때에는 각도법 대신 호의 길이를 기준으로 각을 측정하는 방법을 사용합니다. 이를 호도법(Radian)이라고 부릅니다.

호도법은 호의 길이가 ${1}$이 되는 부채꼴의 각을 기준으로 각을 측정합니다. 호도법의 단위 각을 측정하는 방법을 살펴봅시다.
위와 같이 원점에 중심을 둔 반지름이 ${1}$인 단위 반원을 그립니다. 반원의 호 길이를 비교하기 위해 ${x}$축에 원점에서 크기가 ${1}$인 벡터를 배치했습니다.

반원의 호 길이를 재기 위해 위와 같이 반원의 왼쪽 끝 점을 원점으로 평행이동 시켜봅시다.

그리고 반원의 왼쪽 끝을 고정한 후, ${x}$축의 양의 방향으로 반원의 오른쪽 끝점을 잡아당겨 ${x}$축 위에 쭉 펼친후, 길이를 ${x}$축 상의 단위 벡터와 함께 비교해봅시다.
반원의 호의 길이는 단위 벡터의 길이 ${1}$보다 대략적으로 ${3.14}$배 더 큰데, 정확한 값을 구할 수는 없습니다. 바로 이것이 3.141592...로 이어지는 무리수인 원주율 ${\pi}$입니다.

${180˚}$에 해당하는 반원의 호 길이가 파이임을 알았으니, 이번에는 거꾸로 호의 길이가 ${1}$인 부채꼴의 중심각은 몇 도인지 생각해봅시다.
호의 길이를 ${1}$으로 설정하면, 위 이미지같은 부채꼴이 나오는데, 이 부채꼴의 각이 바로 호도법에서 사용하는 각의 기준인 ${1rad}$입니다.
${1rad}$은 각도로 환산하면 약 ${52.2958˚}$가 되며 이 역시 ${\pi}$와 같은 무리수입니다.
\[\pi = 180\]${180˚}$에 해당하는 반원의 각을 라디안으로 표현하면 얼마인지 알아봅시다.
반원의 호 길이는 ${\pi}$이므로 각 역시 라디안을 기준으로 ${\pi}$배 만큼 커질 것입니다. 따라서 각도법과 호도법 사이에는 위와 같은 대응 관계가 성립합니다.
\[1 = \frac{\pi}{180}(rad)\\ 1(rad) = \frac{180}{\pi}\]- 30 = ${\frac{\pi}{6}}$
- 45 = ${\frac{\pi}{4}}$
- 60 = ${\frac{\pi}{3}}$
- 90 = ${\frac{\pi}{2}}$
- 180 = ${\pi}$
- 360 = ${2\pi}$
실무에서 사용하는 삼각함수는 모두 호도법을 사용하지만, 일상생활에서 회전을 표현할 때는 각도법이 친숙합니다. 회전이라는 행동을 표현할 때는 가급적이면 각도법을 사용할 것입니다.
레퍼런스(Reference)
- 이득우의 게임수학 : (http://www.yes24.com/Product/Goods/107025224)