개요
후디니에서 삼각함수를 사용하는 방법에 대해 소개합니다.
삼각함수를 시각화 하여 여러개의 포인트를 이어 그래프를 그릴 수 있도록 준비 할 것입니다.
addpoint 함수
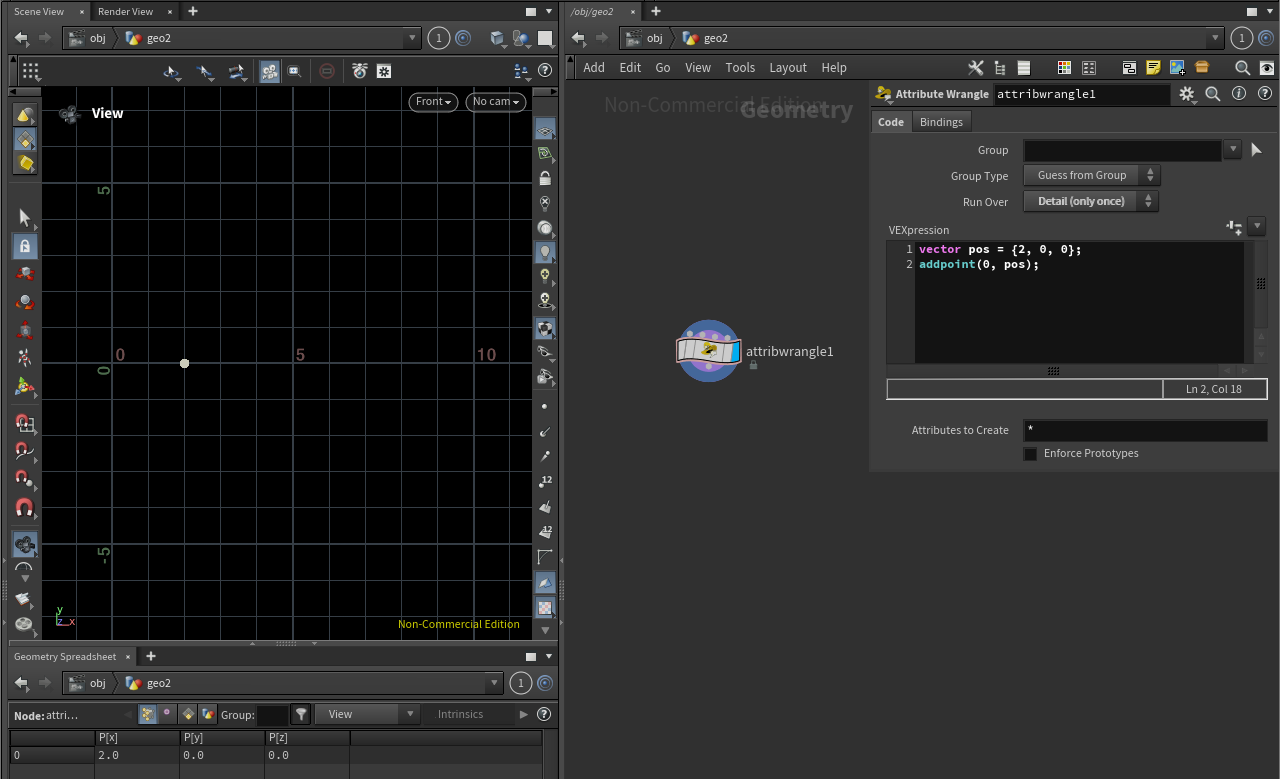
addpoint(0, {0, 0, 0});
vector pos = {2, 0, 0};
addpoint(0, pos);
Vex에서 addpoint(,) 함수를 사용하면 원하는 위치 pos 에 포인트를 생성 할 수 있습니다.
for 반복문
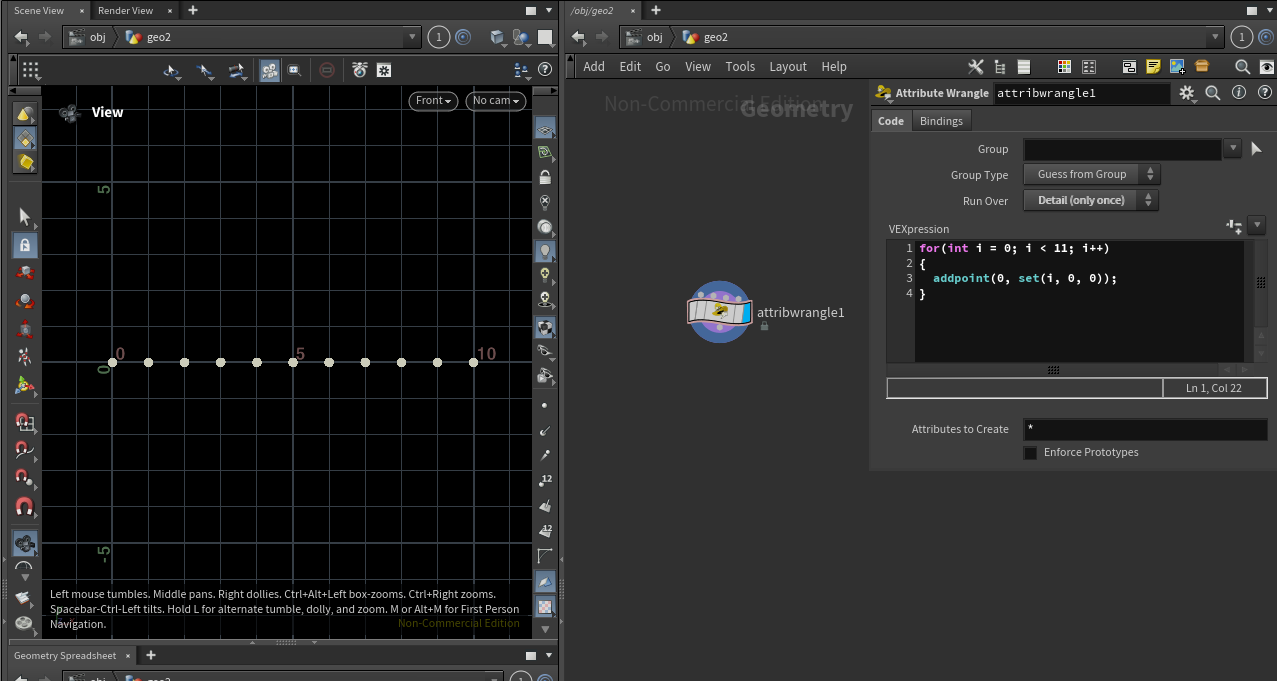
for(int i = 0; i < 11; i++)
{
addpoint(0, set(i, 0, 0));
}
‘for’ 반복문으로 ${1}$ 만큼 ${x}$축으로 이동한 포인트를 생성합니다. i < 11 이라서 최대 ${10}$개의 포인트를 생성합니다.
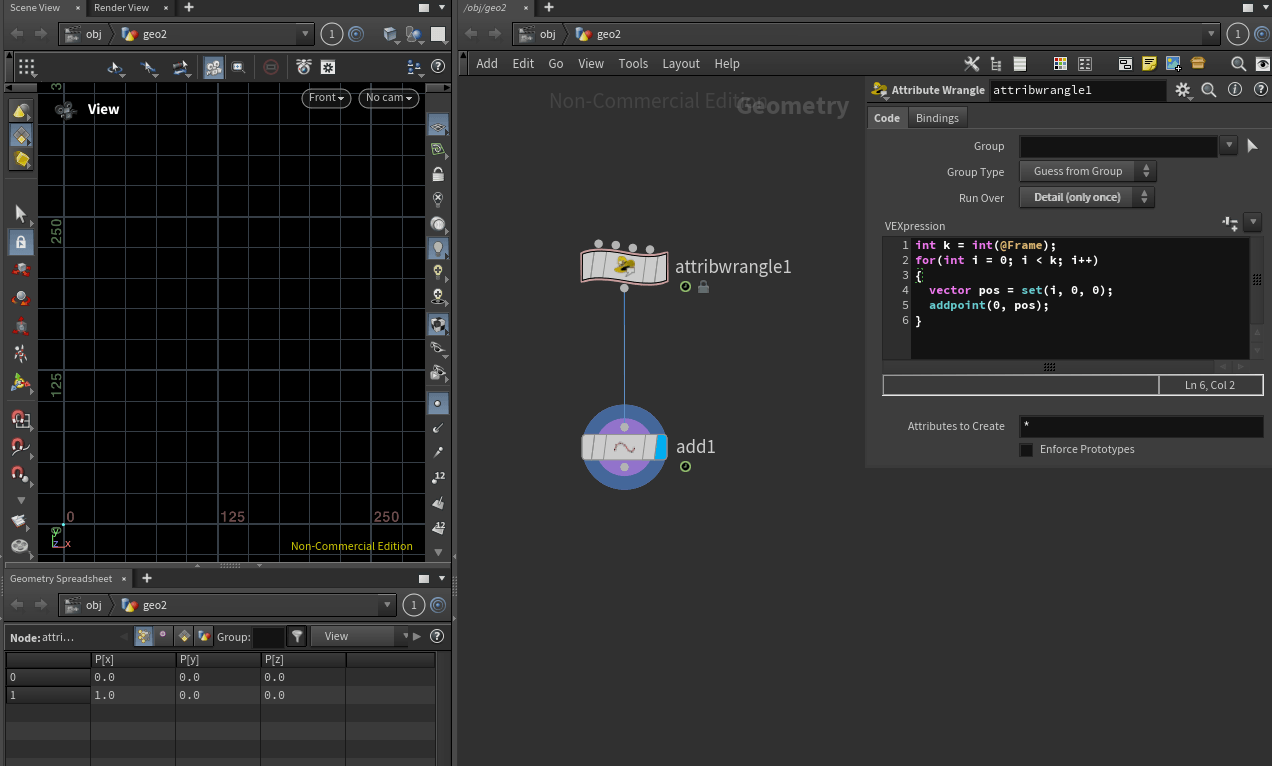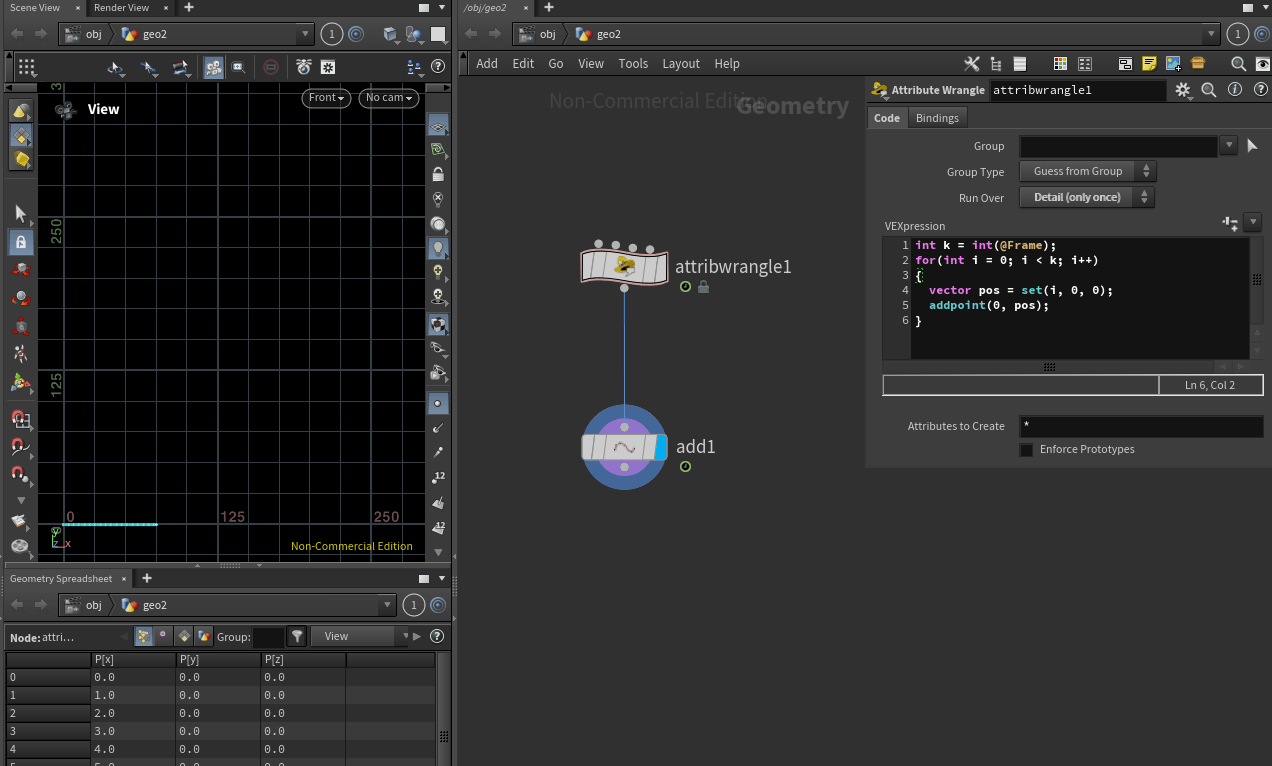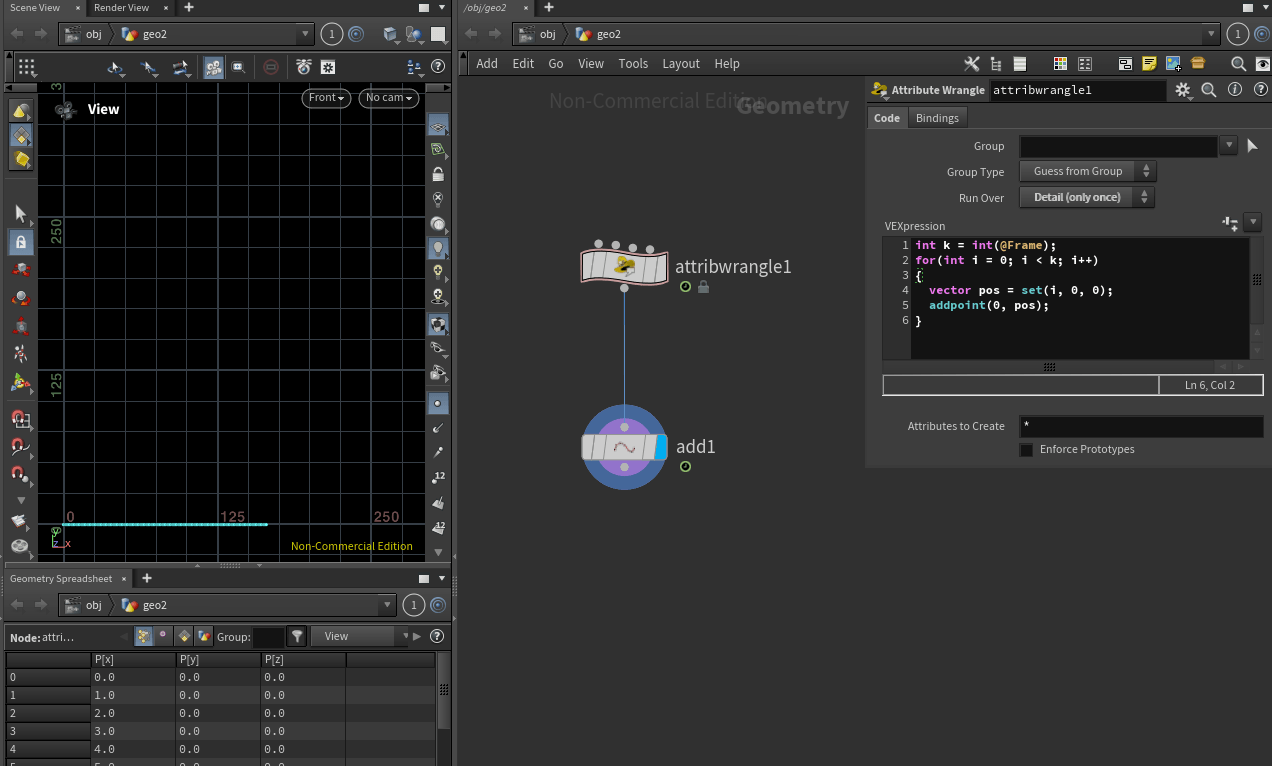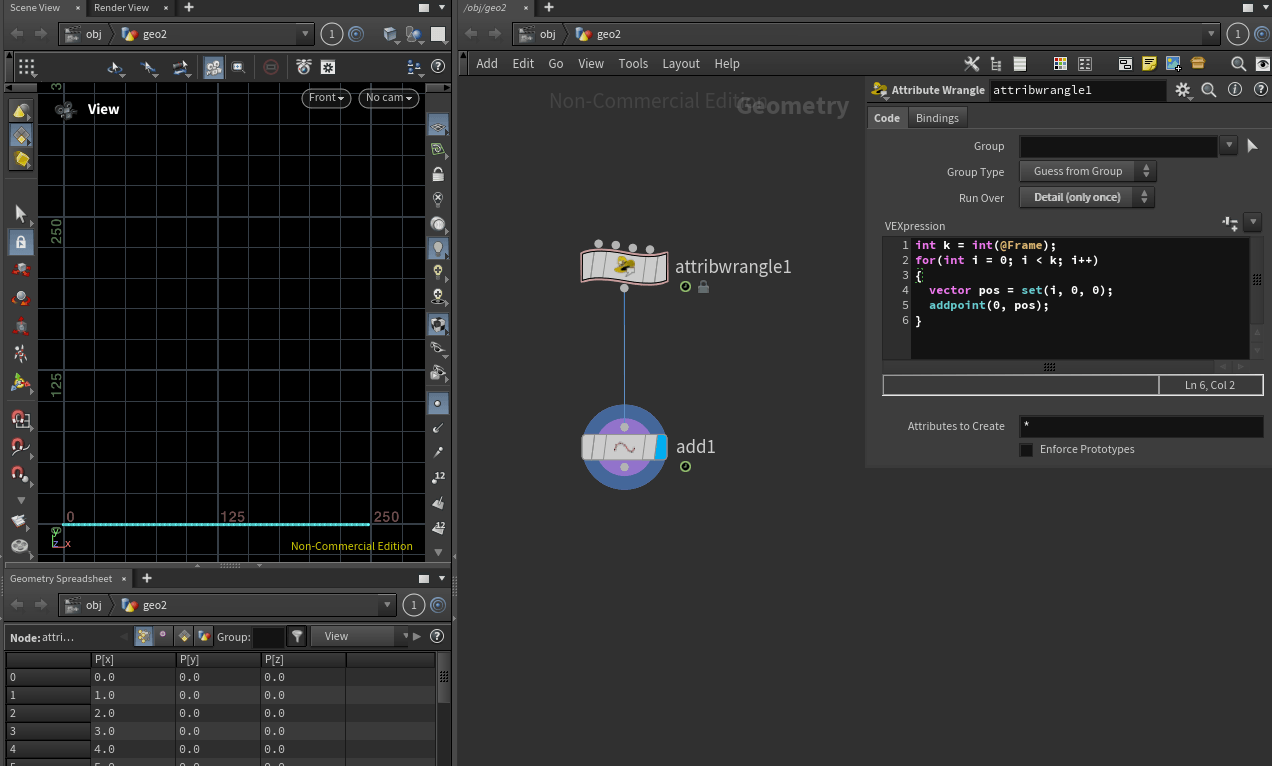
int k = int(@Frame);
for(int i = 0; i < k; i++)
{
vector pos = set(i, 0, 0);
addpoint(0, pos);
}
@Frame 을 사용하여 프레임 값 만큼 포인트 숫자가 증가하도록 애니메이션 시킬 수 있습니다.
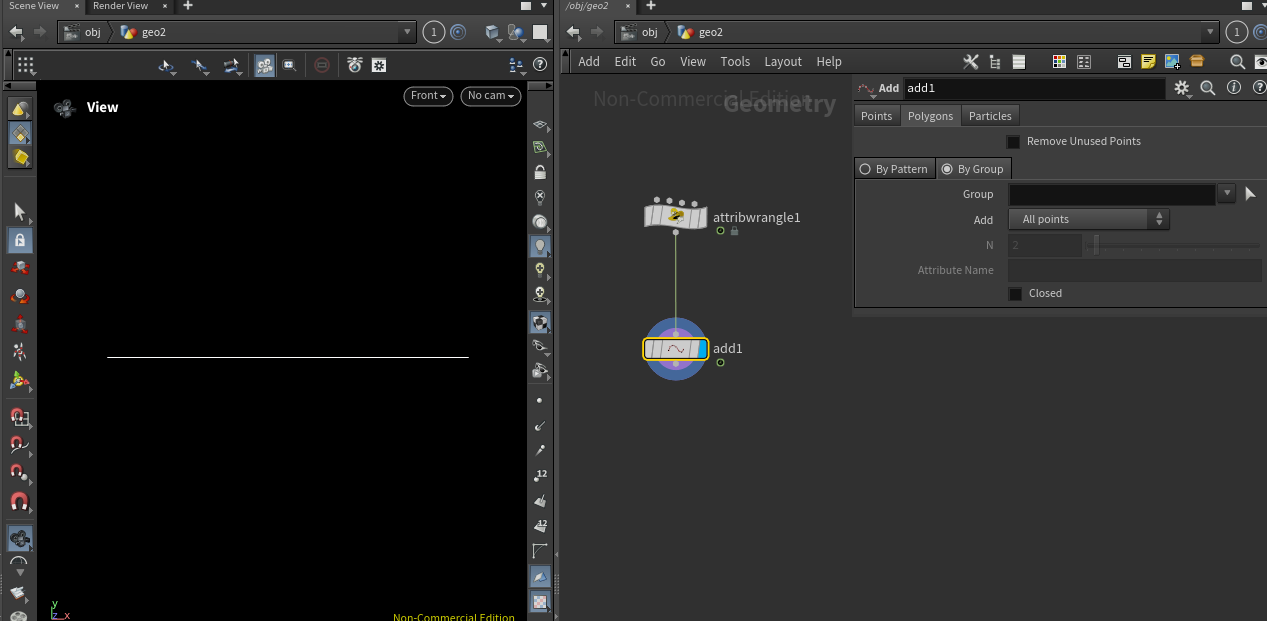
증가한 포인트들을 더하기(Add) 노드를 사용해서 ‘By Group’ 으로 지정해주면 선분이 됩니다.
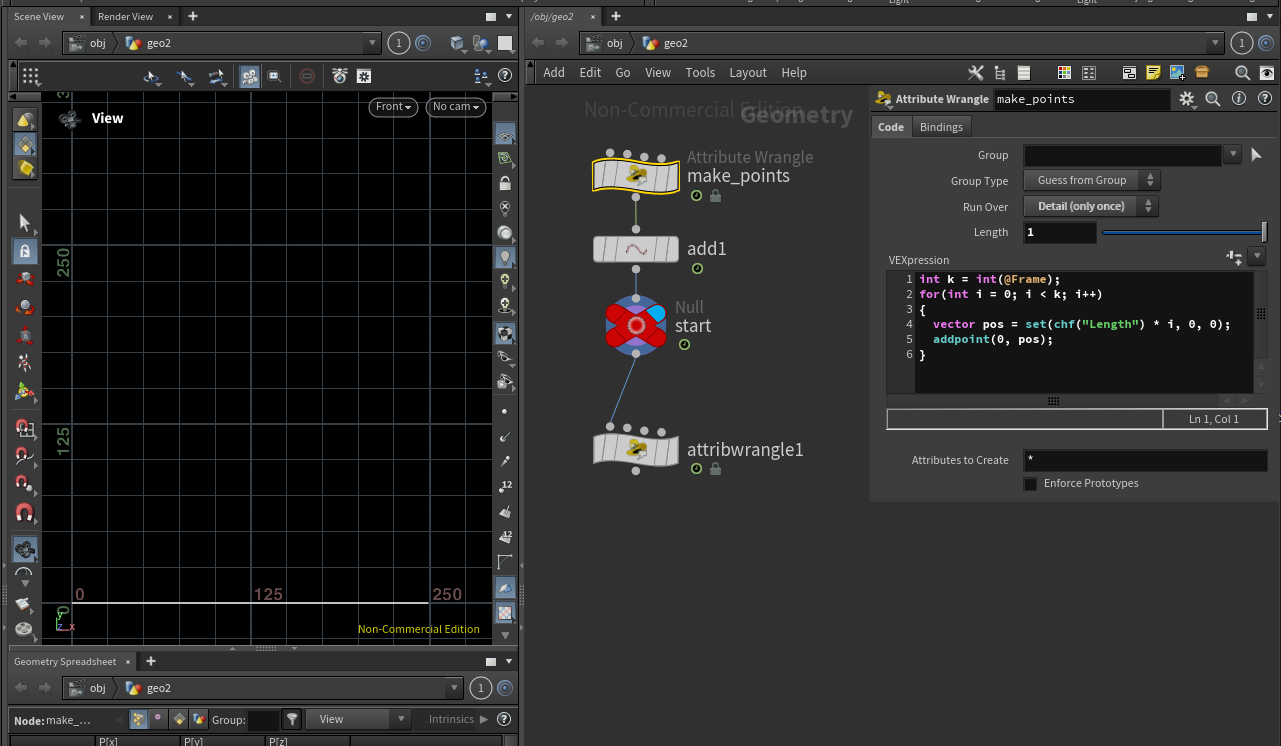
다음은 선분의 늘어나는 길이를 제어하고자 합니다.
선분은 포인트와 포인트의 간격으로 결정됩니다.
int k = int(@Frame);
for(int i = 0; i < k; i++)
{
vector pos = set(chf("Length") * i, 0, 0);
addpoint(0, pos);
}
i++ 구문으로 ${1}$ 만큼 ${x}$축으로 이동한 포인트가 생성됩니다. Length 파라미터를 추가하고 포인트가 생성되는 포지션 pos의 ${x}$값인 i와 곱합니다.
포지션 pos의 ${x}$값은 i * length 가 되어 포인트 사이의 간격을 ${1}$보다 크거나 작은 값으로 제어 할 수 있게 되었습니다.
삼각함수를 시각화 하여 여러개의 포인트를 이어 그래프를 그릴 수 있도록 준비가 끝났습니다.
삼각함수(Trigonometric functions)
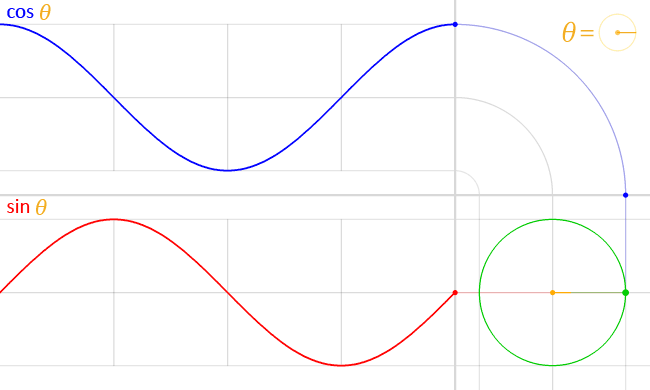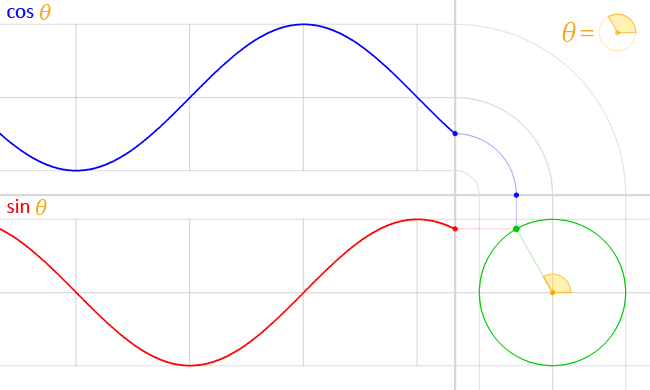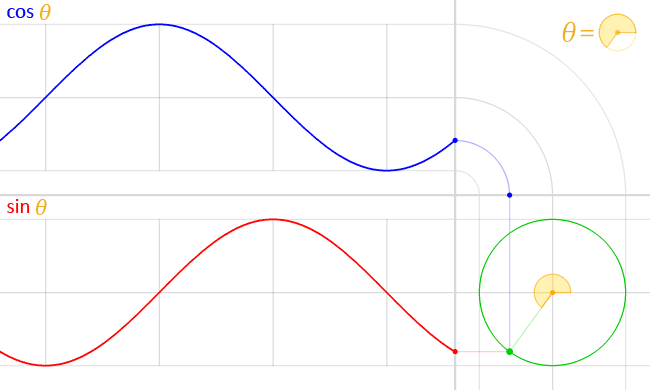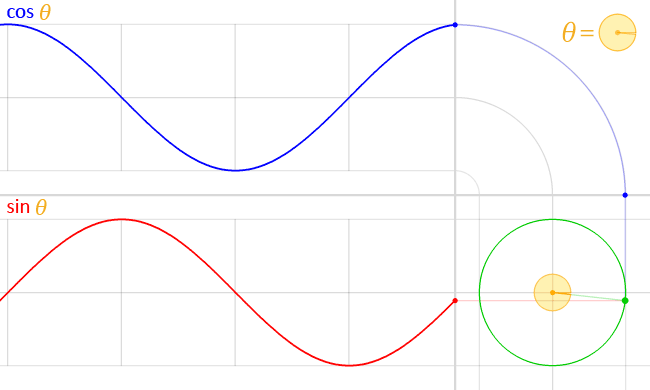
- 게임 수학 입문 - 삼각함수 : (https://walll4542developer.github.io/math/Trigonometric-functions)
삼각함수에 대한 자세한 설명은 위 링크를 참고해주세요.
사인(sine) 함수 그래프
삼각함수중에서 가장 쉬운 사인(sine) 함수 그래프 부터 그려보도록 하겠습니다.
위와 같이 노드를 정리해줍시다.
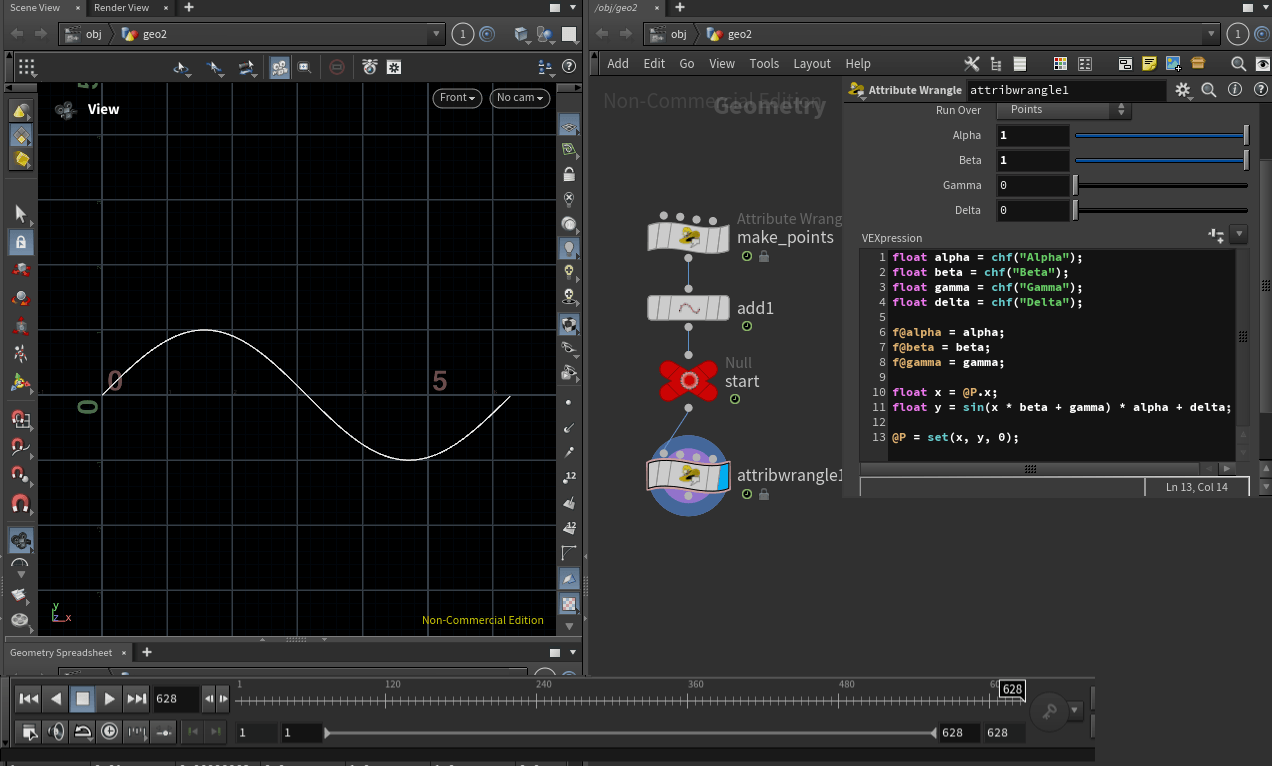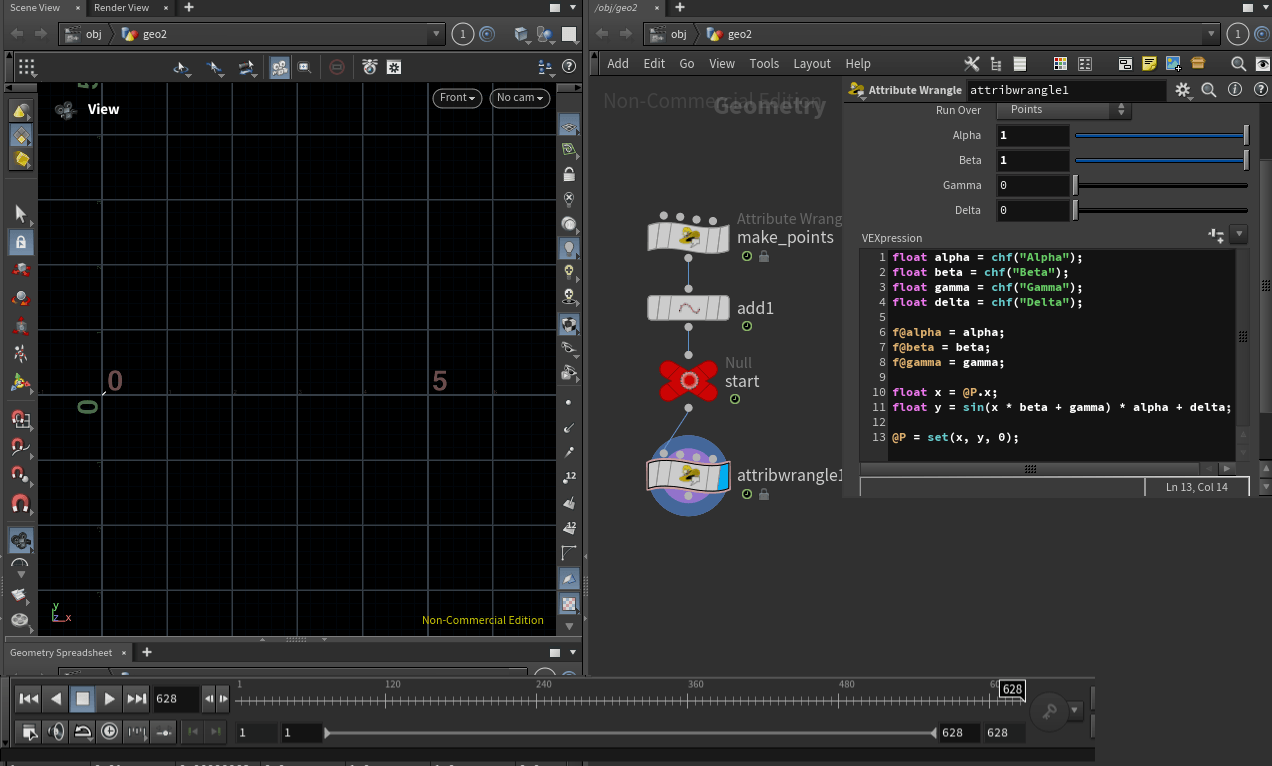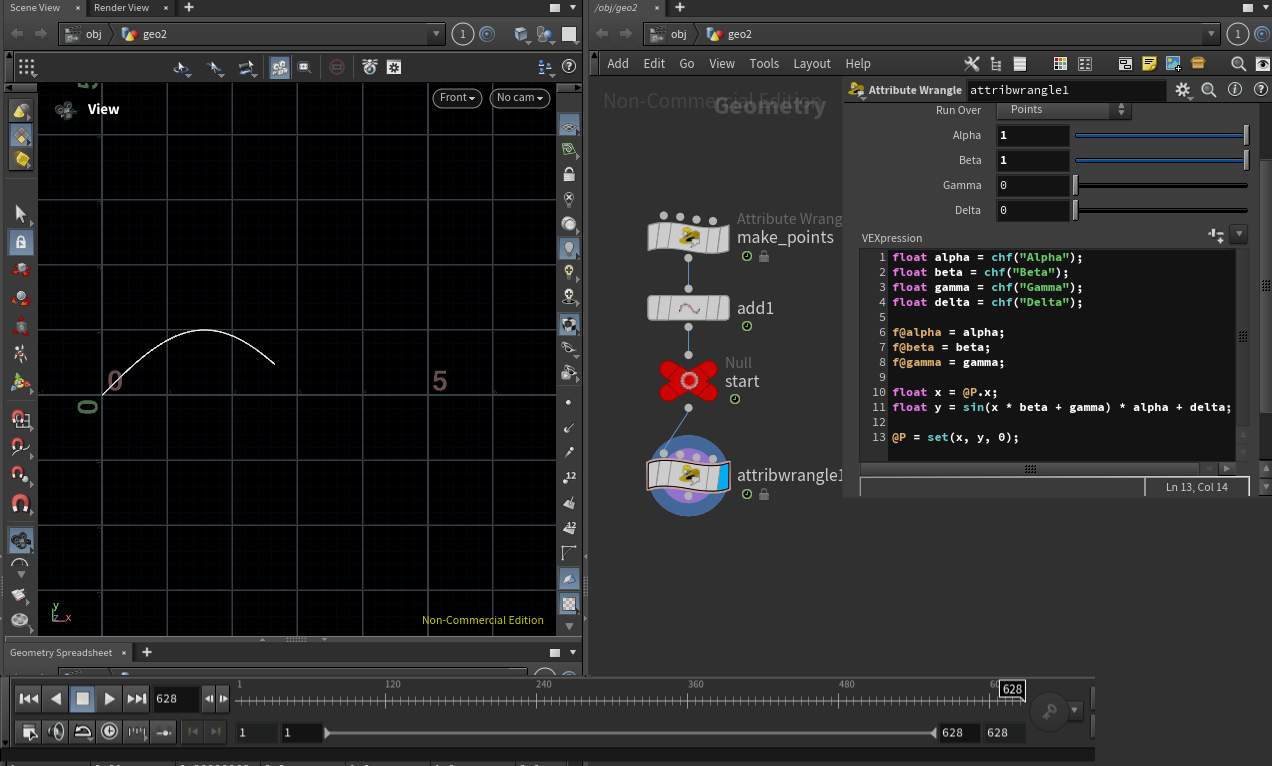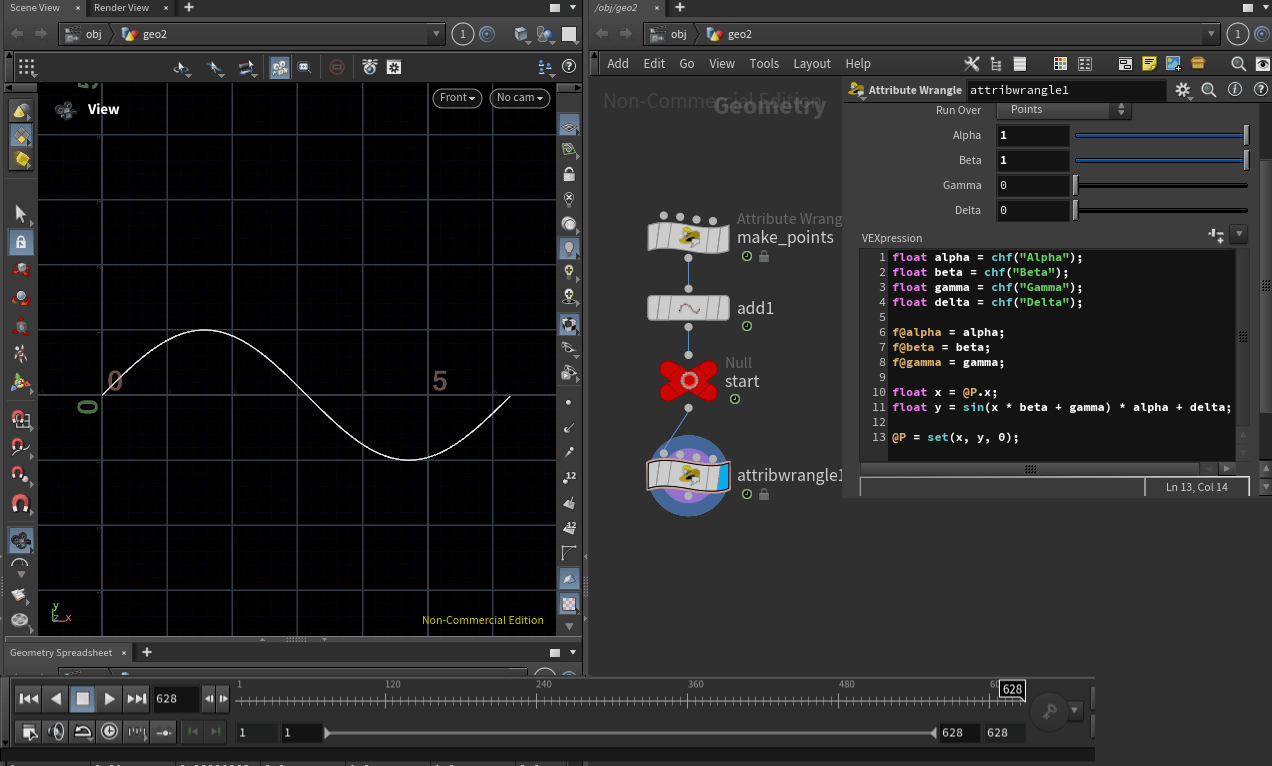
\[y = sin(\theta * |\beta| + \gamma) * \alpha + \delta\]
- ${\alpha}$(알파)는 진폭을 조절 합니다.
- ${\beta}$(베타)는 파장을 조절 합니다.
- ${\gamma}$(감마)는 그래프를 수평이동 합니다.
- ${\delta}$(델타)는 그래프를 수직이동 합니다.
삼각함수 그래프의 수식을 Vex로 변환해봅시다.
\
float alpha = chf("Alpha");
float beta = chf("Beta");
float gamma = chf("Gamma");
float delta = chf("Delta");
float x = @P.x;
float y = sin(x * abs(beta) + gamma) * alpha + delta;
@P = set(x, y, 0);
삼각함수의 ${\theta}$ 값이 곧 @P.x의 ${x}$ 값 입니다.
위 이미지 처럼 사인 함수의 주기를 모두 표현 하고 싶습니다.
사인 함수는 ${2\pi}$의 주기를 가집니다.

@Frame 을 사용하여 프레임 값 만큼 포인트 숫자가 증가한다는 점을 생각했을 때,
프레임 값을 ${2\pi}$ 의 배수로 설정해주면 한 번의 주기를 모두 표현 할 수 있습니다.
그래서 프레임 값을 ${2\pi * 100 \approx 628}$으로 설정했습니다.
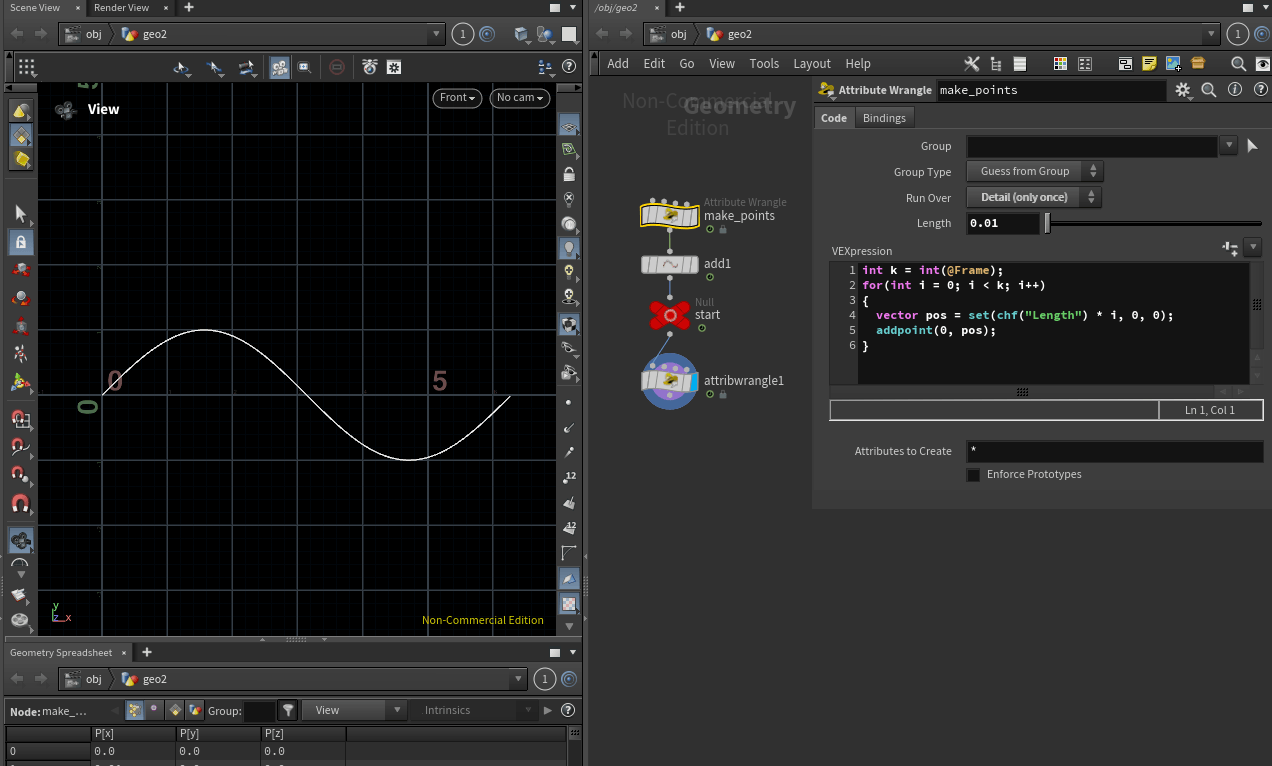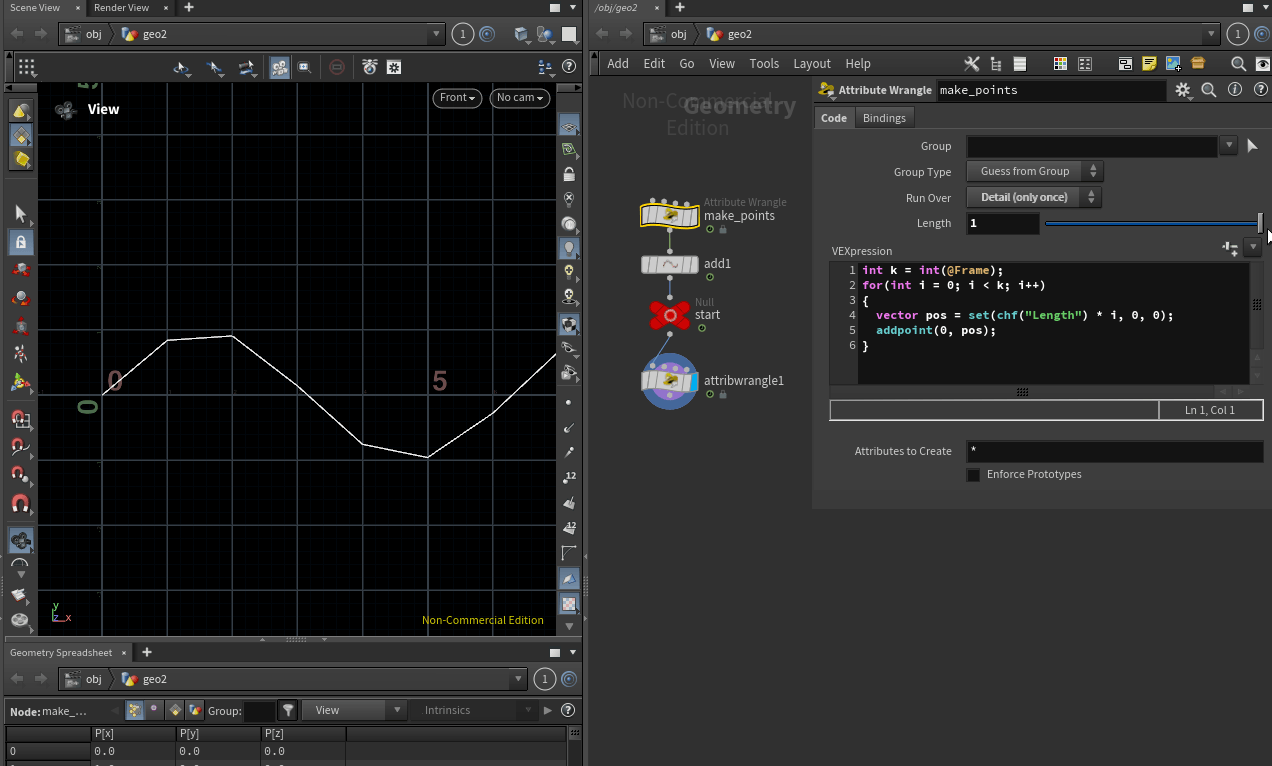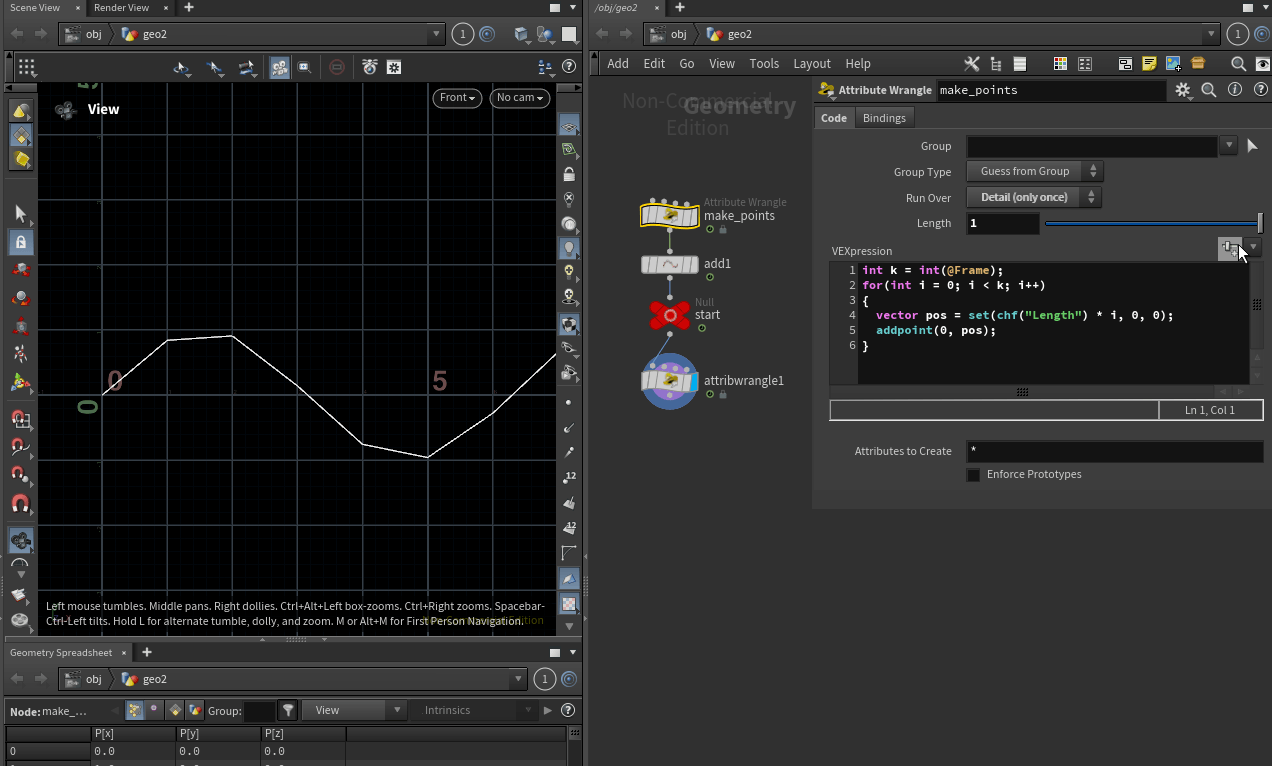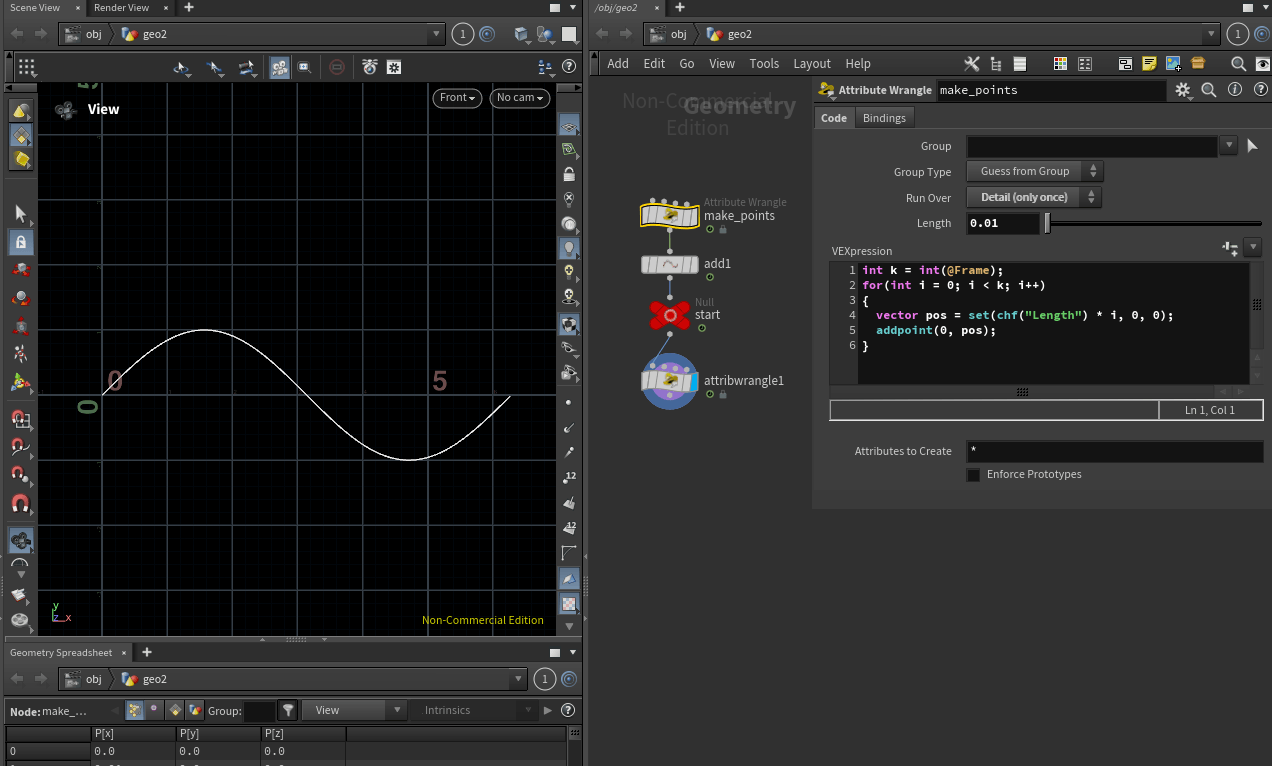
프레임 값을 ${100}$배 증가 시켰으니 Length 값은 반대로 ${1/100}$ 인 ${0.01}$으로 설정 해주면 그래프를 보기 편합니다.
Length 값은 생성하는 포인트 사이의 간격을 의미하며, 위 이미지 처럼 포인트 사이의 간격이 커졌으니 그래프의 해상도가 떨어지기 때문입니다.
다음은 위 이미지처럼 삼각함수의 그래프의 수직, 수평 좌표와 연동되어 움직이는 오브젝트를 만들어 보겠습니다.
삼각함수를 시각적으로 이해하기 쉽도록 특정 좌표를 잡고 오브젝트를 붙이는 작업입니다.
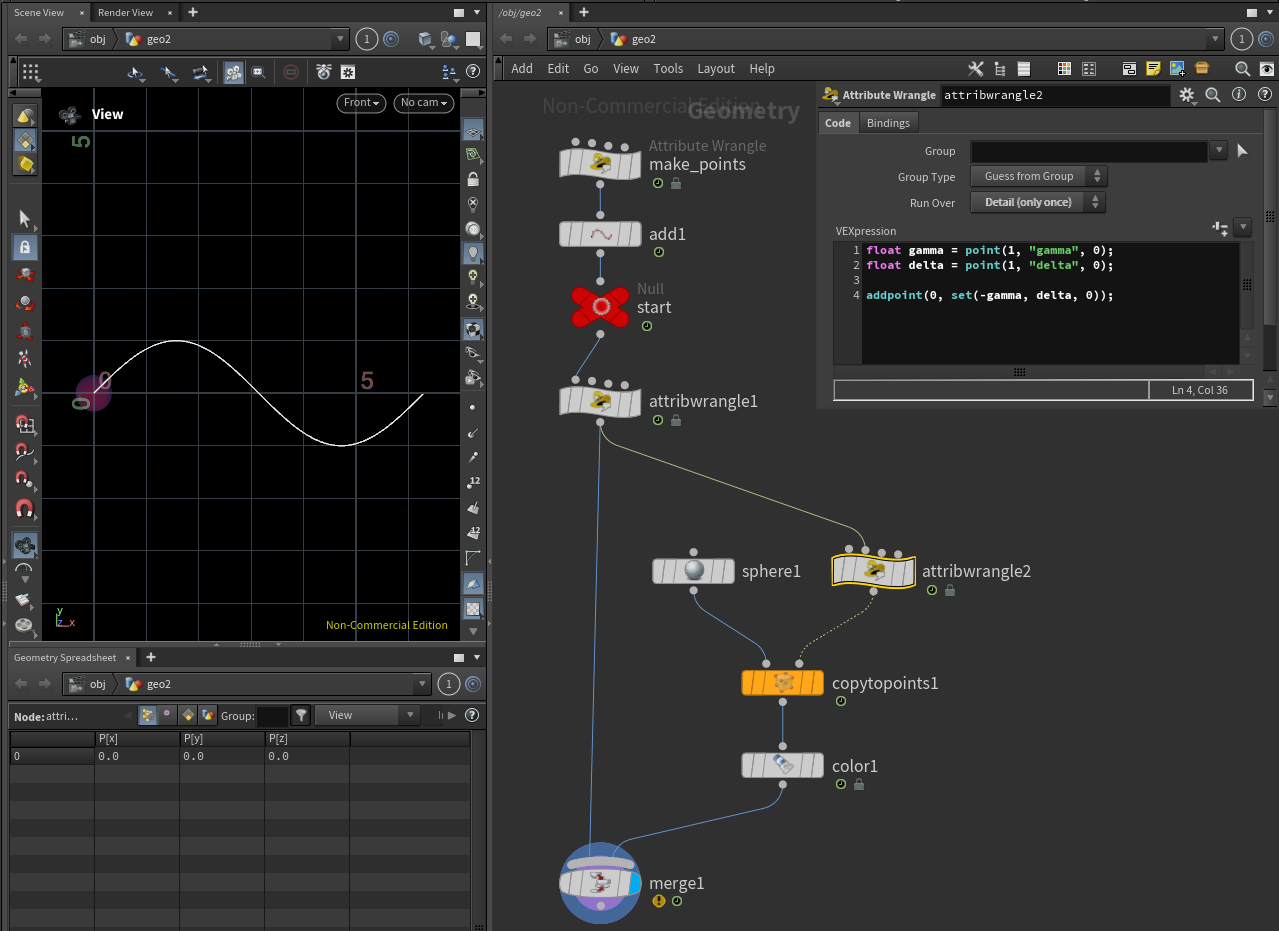
float gamma = point(1, "gamma", 0);
float delta = point(1, "delta", 0);
addpoint(0, set(-gamma, delta, 0));
어트리뷰트 랭글 노드를 하나 더 연결하고 위와 같이 Vex를 작성합시다.
addpoint(,) 함수를 사용하여 ${x}$축은 ${-\gamma}$, ${y}$축 값은 ${\delta}$로 설정한 포인트를 생성합니다.
${\gamma}$에 음수 부호를 붙인 이유는 삼각함수의 그래프의 ${-\gamma}$ 는 수평, ${\delta}$는 수직 좌표와 연동되어 움직여야 하기 때문입니다.
${\beta}$에 절댓값 기호${\mid\mid}$를 붙인 이유는 ${\beta}$가 음수가 될 경우 그래프의 ${y}$축이 반전되기 때문입니다.
코사인(cosine) 함수 그래프
float x = @P.x;
float y = cos(x * abs(beta) + gamma) * alpha + delta;
@P = set(x, y, 0);
간단합니다. 사인 함수를 코사인 함수로 바꿔주면 됩니다.
노이즈(noise) 함수 그래프
float x = @P.x;
float y = noise(x * abs(beta) + gamma) * alpha + delta;
@P = set(x, y, 0);
같은 방식으로 노이즈(noise) 함수로 바꿀 수도 있습니다.
noise() 함수로 변경할 경우 위 이미지 처럼 랜덤한 곡선 패턴이 나타납니다. 이는 후디니에서 제공하는 난수로 만들어진 파동 그래프입니다.
레퍼런스(Reference)
- TWA 후디니의 정석 : https://www.youtube.com/@TWAHOUDINI
- 게임 수학 입문 - 삼각함수 : https://walll4542developer.github.io/math/Trigonometric-functions
- Vex : https://www.sidefx.com/docs/houdini/vex/index.html
- 나무위키/파동 : https://namu.wiki/w/%ED%8C%8C%EB%8F%99