최우영

Junior Technical Artist / 3d WEEABOO This blog use personal issue only.

파동의 합성

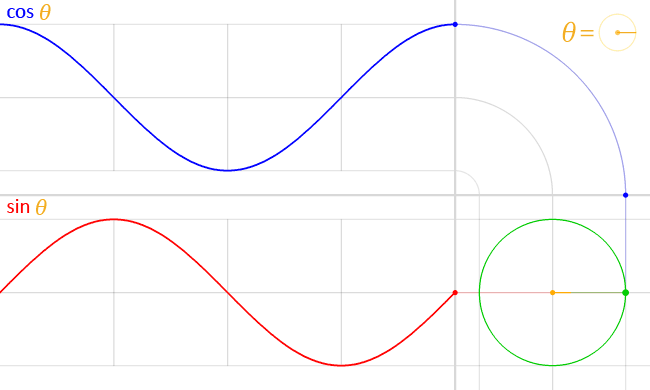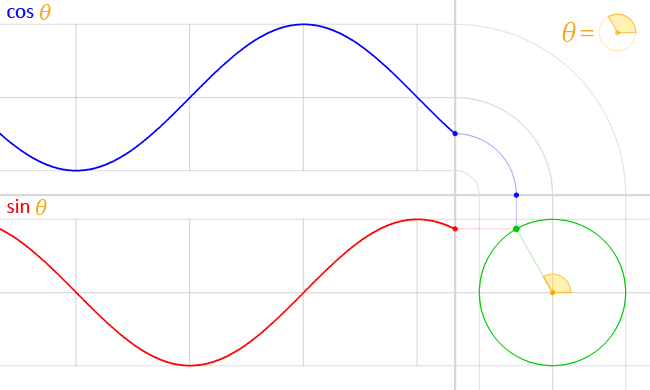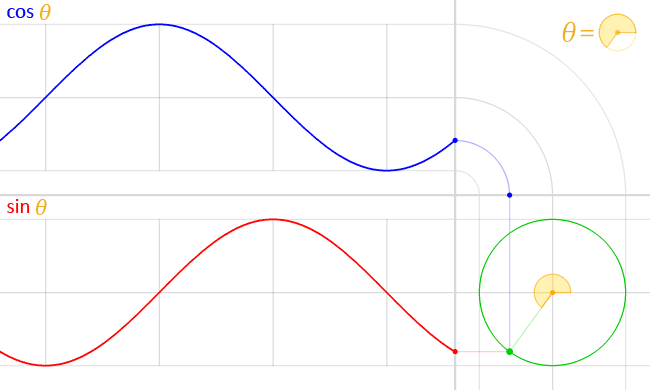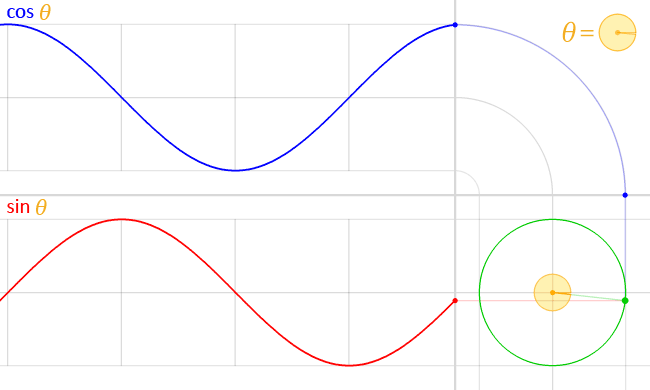
Houdini-Beginner

sin(), cos() 는 삼각 함수이며 위 처럼 진동하고 일정한 주기를 가지는 파동의 형태를 가지고 있습니다.

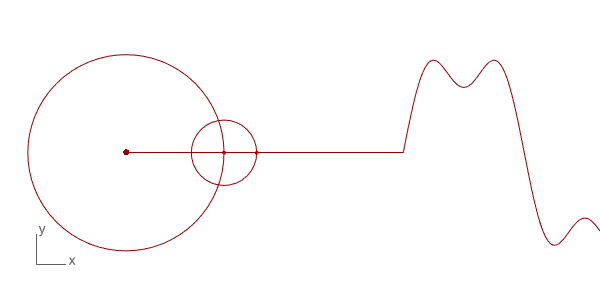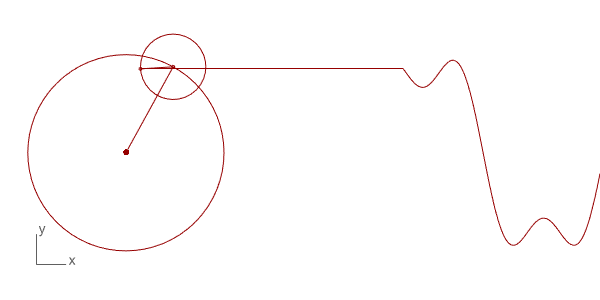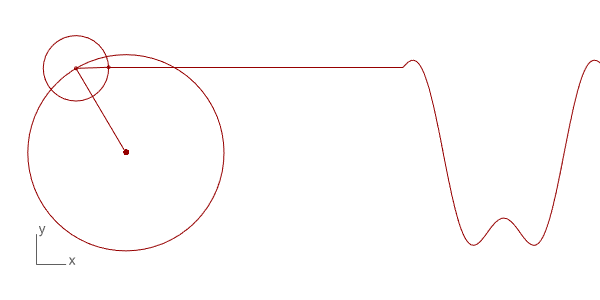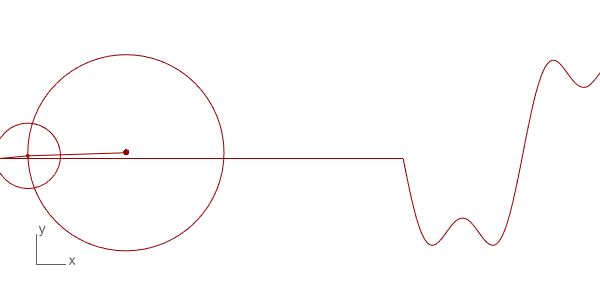
Houdini-Beginner

이전 포스트(링크)에서 배웠던 noise() 함수는 사실 위 이미지 처럼 여러 개의 삼각함수가 만드는 파동의 합성으로 이루어져 있습니다.

반대로 모든 파동은 여러가지 파동으로 분해 할 수 있습니다. 이를 푸리에 변환(fourier transform) 이라고 하는데 나중에 다루도록 하겠습니다.

영점 중앙 노이즈

합성의 결과를 알아보기 쉽도록 noise() 함수의 시작점을 항상 ${0}$에서 시작하도록 보정해줄 수 있습니다. 이처럼 시작점이 ${0}$인 노이즈를 영점 중앙 노이즈(Zero-Centered noise)라고 합니다.

float x = @P.x;
// float y = noise(x * abs(beta) + gamma) * alpha + delta;
float y = noise((x * abs(beta) + gamma) * alpha) + delta;
@P = set(x, y, 0);

noise() 함수가 항상 ${0.5}$에서 시작하기 때문에 ${\delta}$ 값을 ${-0.5}$로 설정하고 noise() 함수에 ${* \alpha}$ 연산을 포함하면 됩니다.

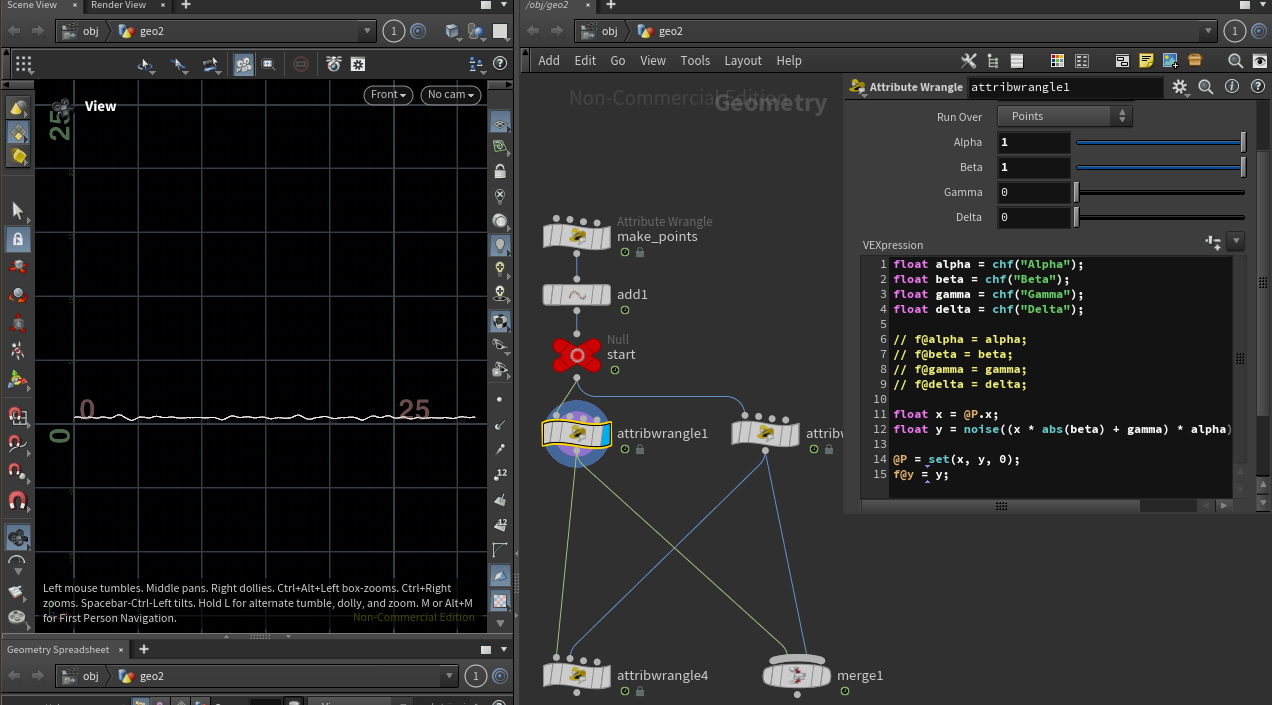
Houdini-Beginner

float y = sin(x * abs(beta) + gamma) * alpha + delta;
f@y = y;

float y = noise((x * abs(beta) + gamma) * alpha) + delta;
f@y = y;

sin() 과 noise() 두 가지의 파동을 합성하기 위해 함수 그래프의 @P.y 값을 어트리뷰트(attribute) f@y 값으로 내보냅니다.

@ptnum

float a = point(0, "y", @ptnum);
float b = point(1, "y", @ptnum);

point(,,) 함수를 사용하여 f@y 값을 받아옵니다.

point("주소","어트리뷰트 이름",'포인트 인덱스') // Vex
point("주소", '포인트 인덱스', "어트리뷰트 이름", '어트리뷰트 주소'); // hscript

point(,,) 함수에서 ‘포인트 인덱스’ 자리에 @ptnum 을 사용하면 y의 모든 포인트 인덱스와 값을 그대로 가져올 수 있습니다.

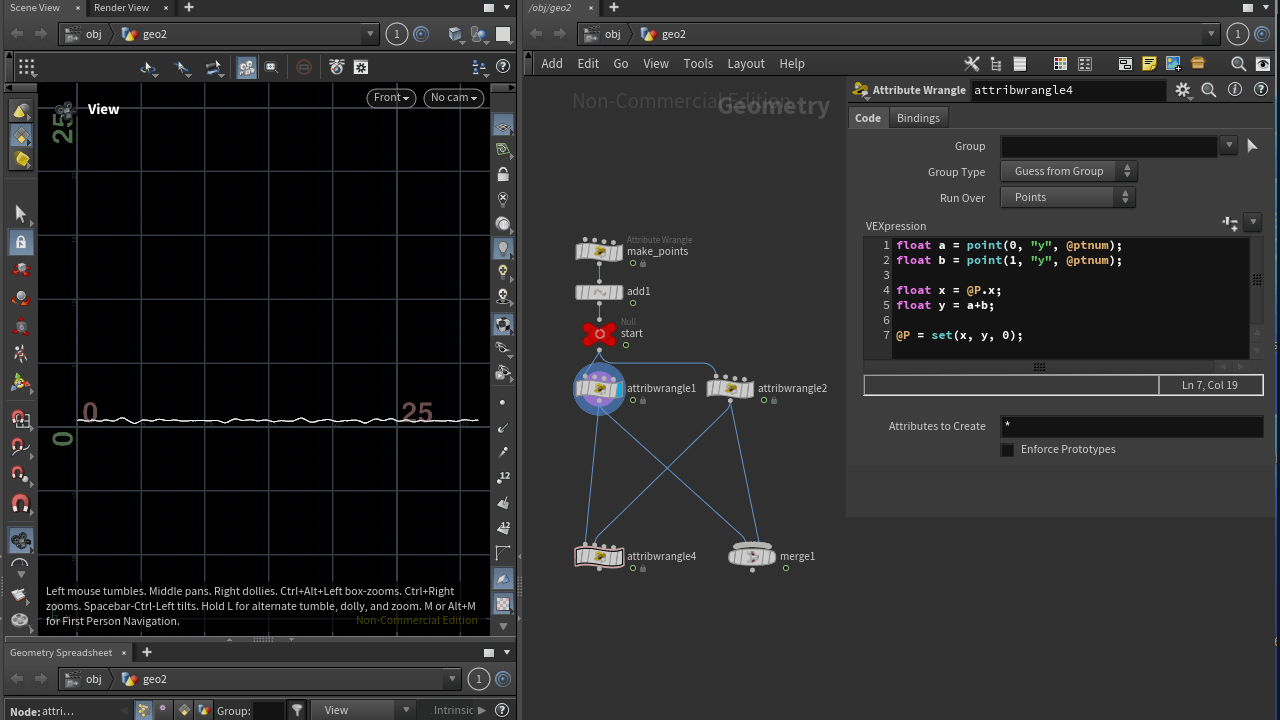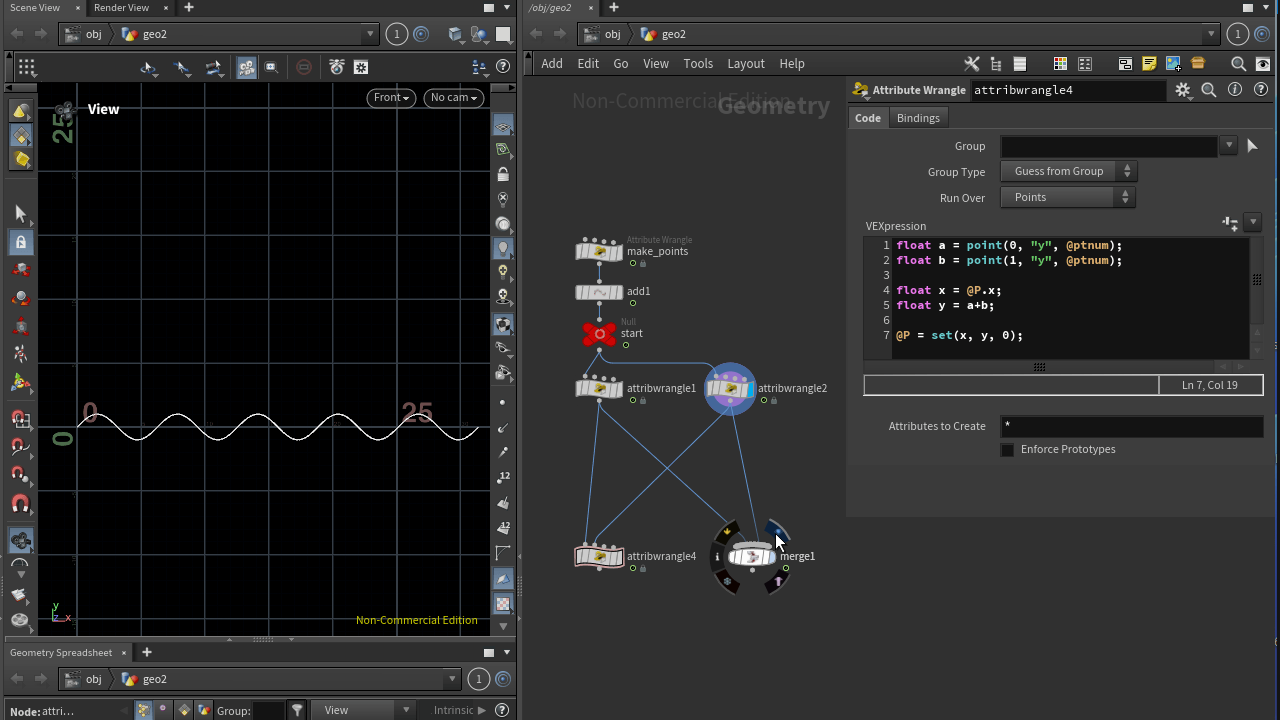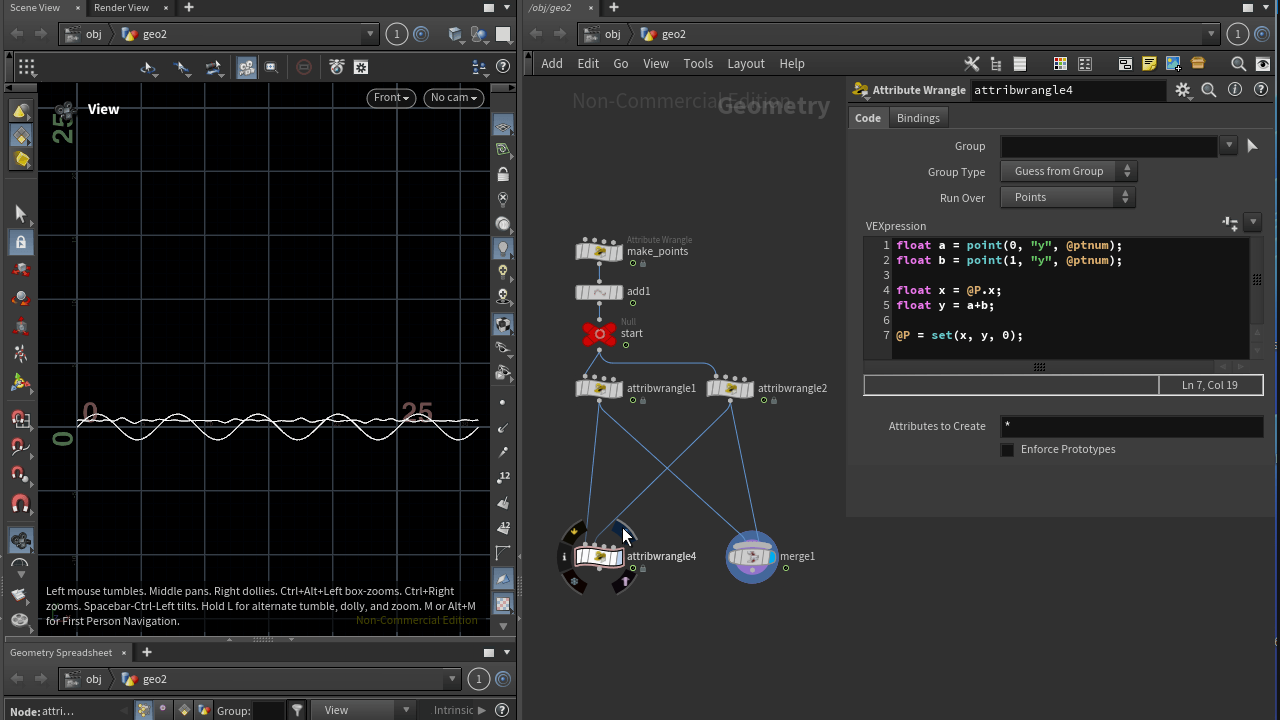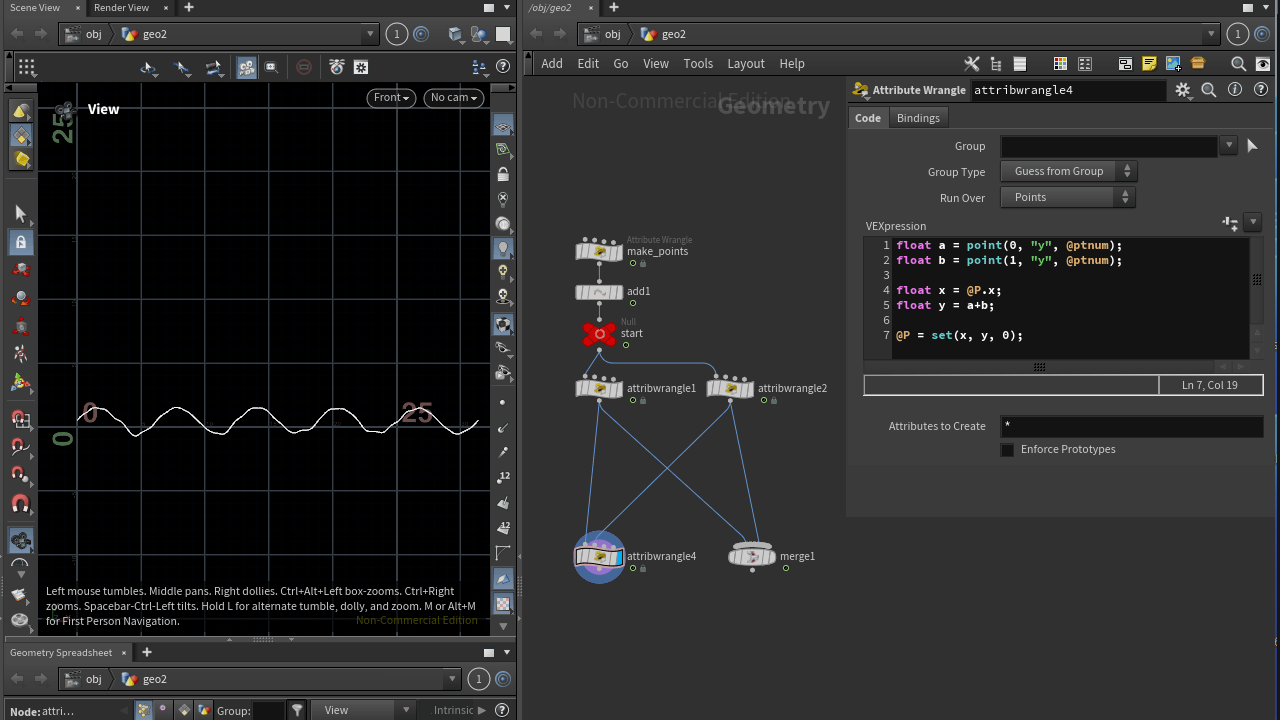
Houdini-Beginner

float a = point(0, "y", @ptnum);
float b = point(1, "y", @ptnum);

float x = @P.x;
float y = a + b;

@P = set(x, y, 0);

두 파동의 합성된 결과를 확인하실 수 있습니다.

Houdini-Beginner

float a = point(0, "y", @ptnum);
float b = point(1, "y", @ptnum);

float alpha = chf("Alpha");
float beta = chf("Beta");

float x = @P.x;
float y = a * alpha + b * beta;

@P = set(x, y, 0);

alpha 와 beta를 추가해서 파동이 얼마나 강하고 약하게 반영될 것인지 조절 할 수 있습니다.

Houdini-Beginner

\[y = sin(\theta * |\beta| + \gamma) * \alpha + \delta\] 
float alpha = chf("Alpha");
float beta = chf("Beta");
// float gamma = chf("Gamma");
float gamma = @Frame * 0.01;
float delta = chf("Delta");
  • ${\alpha}$(알파)는 진폭을 조절 합니다.
  • ${\beta}$(베타)는 파장을 조절 합니다.
  • ${\gamma}$(감마)는 그래프를 수평이동 합니다.
  • ${\delta}$(델타)는 그래프를 수직이동 합니다.

@Frame 값을 사용하여 파동 그래프가 시간의 흐름에 따라 값이 변화하도록 제어할 수도 있습니다.

레퍼런스(Reference)

You May Also Enjoy